A small bead of mass m is carried by a circular hoop having center at O and radius √2m which rotates about a fixed vertical axis. The coefficient of friction between beed and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop. (g=10m/s2)

√5
√10
√15
√30
The correct Answer is:D
The maximum angular speed of the hoop corresponds to the situations when the bead is just about to slide upwards. For the bead to slide upwards.
cos450=xr⇒x=rcos450
mω2(rsin45)−mgsin45≤μN
Where N=mgcos45+mω2(rsin45)sin45
On solving ω≤√(1+μ)g(1−μ)rsin45
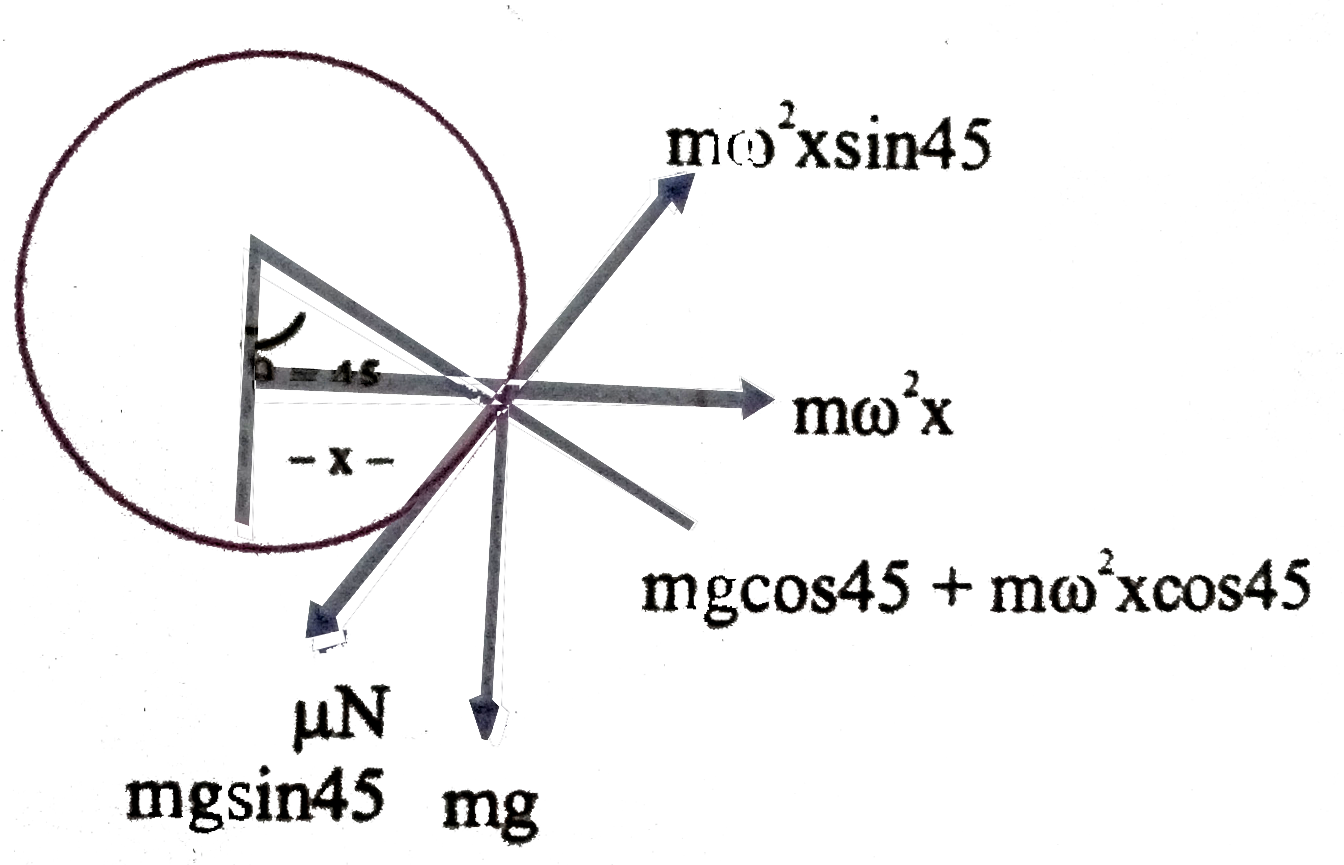
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI PASSAGE3videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI Integer7videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)51videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - CALORIMETRYEXERCISE - Level- II (H.W)11videos
CALORIMETRY
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)54videos
COLLISION
Similar Questions
L shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed ω .The sleeve has mass m and friction coefficient between rod and sleeve is μ.The minimum angular speed ω for which sleeve cannot slip on rod is?
View SolutionFind the maximum speed at which a car can turn round a curve of 30m radius on a level road if coefficient of friction between the tyress and road is 0.4.Takeg=10m/s2.
View Solution
Knowledge Check
- Question 1 - Select One
A small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
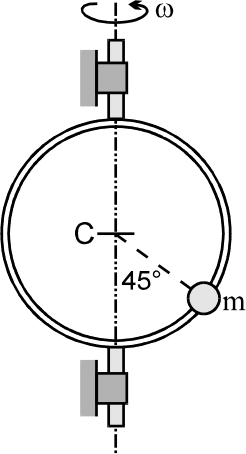 A(5√2)1/2B(10√2)1/2C(15√2)1/2D(30√2)1/2
A(5√2)1/2B(10√2)1/2C(15√2)1/2D(30√2)1/2 - Question 2 - Select One
The coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
A√15ms−1B√3ms−1C√30ms−1D√10ms−1 - Question 3 - Select One
A circular road of radius 1000 m has banking angle 45∘. IF the coefficient of friction is between tyre and road is 0.5, then the maximum safe speed of a car having mass 2000 kg will be
A172m/sB124m/sC99m/sD86m/s
A car is moving on a horizontal circular road of radius 0.1 km with constant speed. If coefficient of friction between tyres of car and road is 0.4, then speed of car may be (g=10m/s2)
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View Solution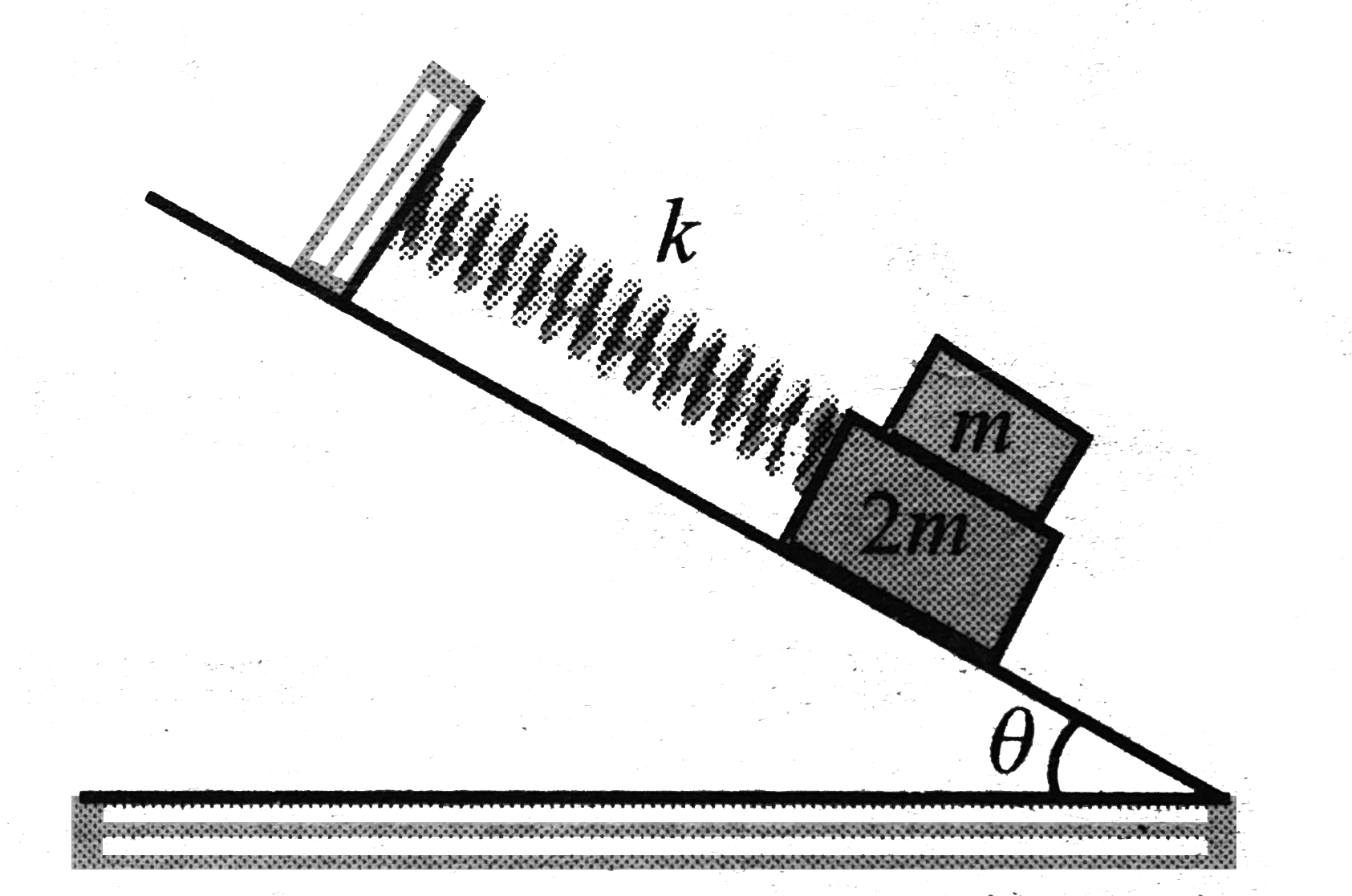
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isView SolutionThe maximum speed with which a car driven round a curve of radius 18 m without skidding (where ,g=10ms−2 and the coefficient of friction between rubber tyres and the roadway is 0.2)is
View Solution

