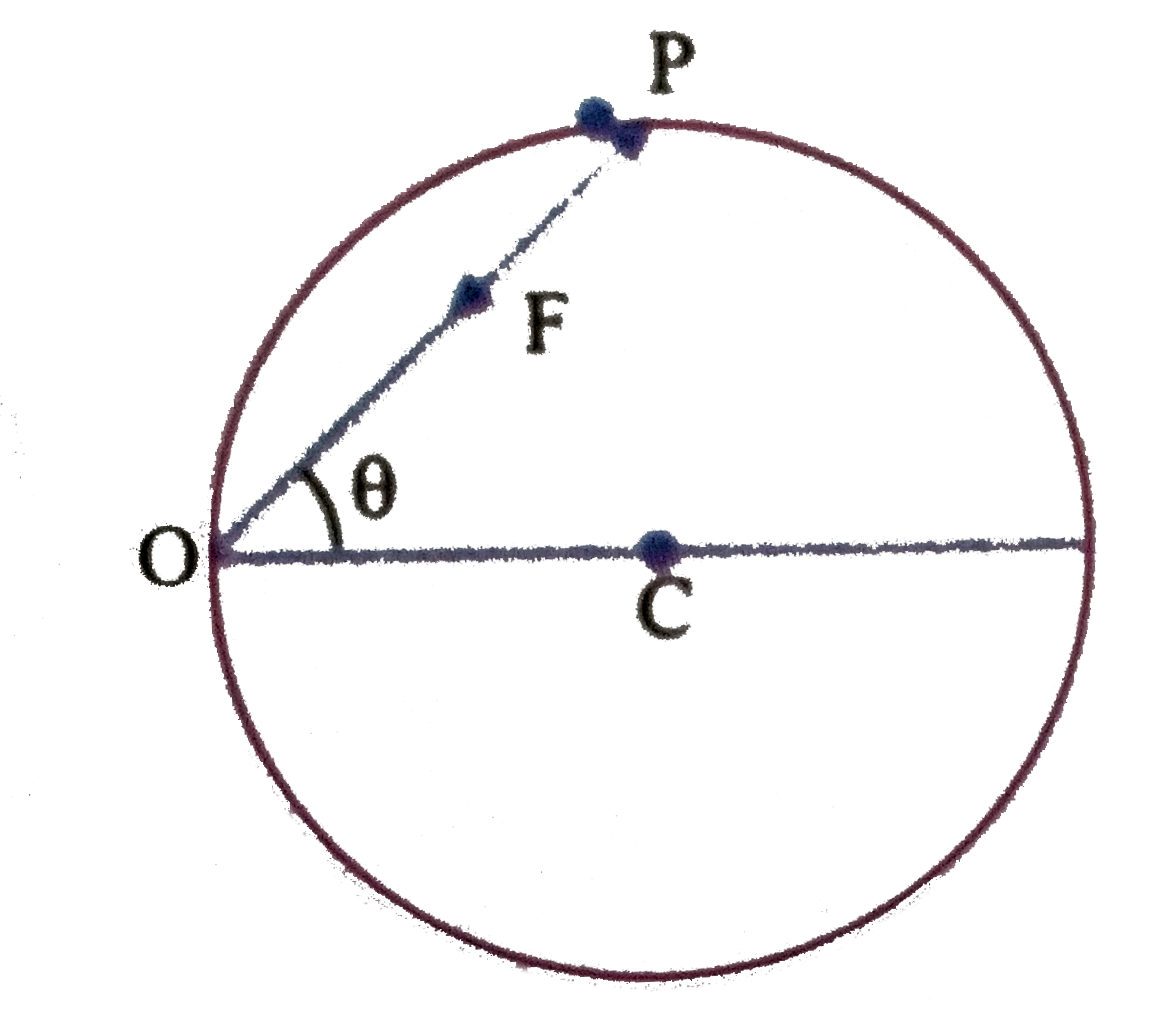
A particle 'P' is moving on a circular under the action of only one force action always toward the fixed point 'O' on the circumference. Find the ratio of d2θdt2 & (dθdt)2
2tanθ
tanθ
tanθ2
tanθ3
The correct Answer is:A
Fcosθ=mRω2,Fsinθ=mat
Angular velocity 'ω' of line joining 'P' and 'C' is
ω=ddt(2θ)=2dθdt,∴dθdt=ω2
Tangential acceleration of particle about 'd'
at=Fsinθm=Rα⇒α=FsinθmR
But α=dωdt=ddt(2dθdt)=2d2θdt2
⇒d2θdt2=α2, Hence d2θdt2=Fsinθ2mR
(dθdt2)2=14ω2=14×FosθmR
On solving d2θ/dt2(dθdt)2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL I(H.W)
43 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI Integer
7 Videos
- CALORIMETRYBOOK - NARAYNACHAPTER - CALORIMETRYEXERCISE - Level- II (H.W)
11 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)
54 Videos
Similar Questions
A charged particle is moving in a circular path under the action of the Lorentz force. How much work is done by the force in one revolution?
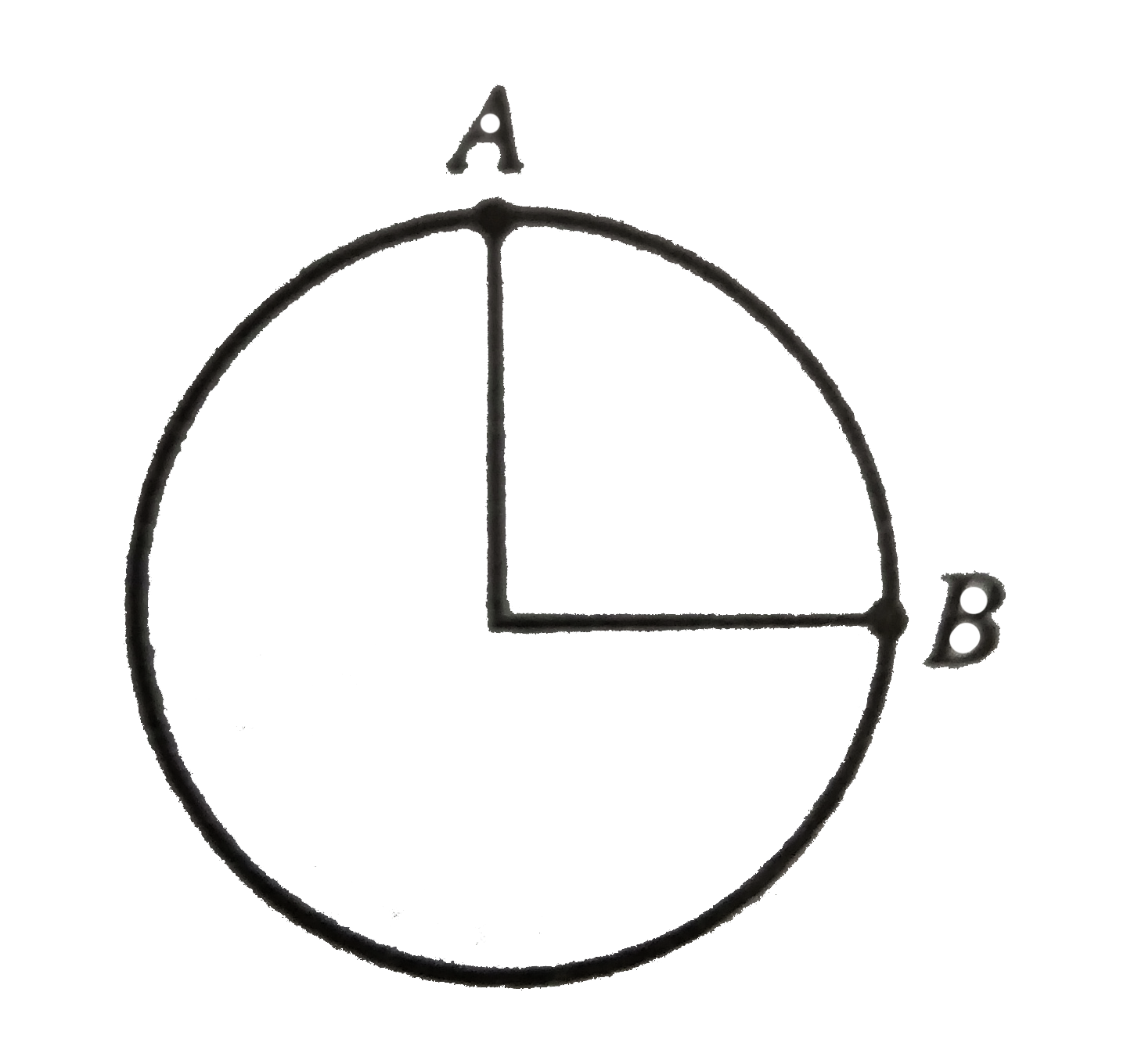
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View Solution
Knowledge Check
A particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
A−32ka2B−k4a2Ck2a2DZeroA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
A2 JB4 JC16 JD8 JA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
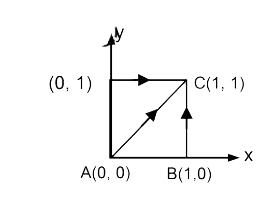 AForce is conservative in natureBWork done by force is 13 when particle moves along path ABCCForce is non conservative in nature and work done along path AC is 1 JDWork done along path ADC is 145J
AForce is conservative in natureBWork done by force is 13 when particle moves along path ABCCForce is non conservative in nature and work done along path AC is 1 JDWork done along path ADC is 145J
A particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionIf x2=t2+! then find d2xdt2
View SolutionFind d(sin2θ.cosθ)dθ
View SolutionIt x=sin2θ, then find dxdt where dθdt)=ω
View SolutionA particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
View Solution
