A horizontal force is applied on a body on a rough horizontal surface produces an acceleration a.If coefficient of friction between the body and surface which is a is reduced to μ/3,the acceleration increses by 2units.The value of μ is
2/3g
3/2g
3/g
1/g
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the forces acting on the body
When a horizontal force F is applied to a body on a rough horizontal surface, the frictional force f opposing the motion can be expressed as:
f=μmg
where μ is the coefficient of friction, m is the mass of the body, and g is the acceleration due to gravity.
Step 2: Write the equation of motion for the initial condition
Using Newton's second law, the net force acting on the body can be expressed as:
F−f=ma
Substituting the expression for friction:
F−μmg=ma(1)
Step 3: Write the equation of motion for the modified condition
When the coefficient of friction is reduced to μ3, the new frictional force becomes:
f′=μ3mg
The new acceleration is a+2. Therefore, the equation of motion becomes:
F−f′=m(a+2)
Substituting the new frictional force:
F−μ3mg=m(a+2)(2)
Step 4: Set up the equations to eliminate F
From equation (1):
F=ma+μmg
Substituting this expression for F into equation (2):
ma+μmg−μ3mg=m(a+2)
Step 5: Simplify the equation
Rearranging the equation gives:
ma+μmg−μ3mg=ma+2m
Subtracting ma from both sides:
μmg−μ3mg=2m
Factoring out mg:
mg(μ−μ3)=2m
This simplifies to:
mg(2μ3)=2m
Step 6: Solve for μ
Dividing both sides by m (assuming m≠0):
g(2μ3)=2
Multiplying both sides by 32g:
μ=2⋅32g=3g
Final Answer
The value of μ is:
μ=3g
When a horizontal force F is applied to a body on a rough horizontal surface, the frictional force f opposing the motion can be expressed as:
f=μmg
where μ is the coefficient of friction, m is the mass of the body, and g is the acceleration due to gravity.
Using Newton's second law, the net force acting on the body can be expressed as:
F−f=ma
Substituting the expression for friction:
F−μmg=ma(1)
When the coefficient of friction is reduced to μ3, the new frictional force becomes:
f′=μ3mg
The new acceleration is a+2. Therefore, the equation of motion becomes:
F−f′=m(a+2)
Substituting the new frictional force:
F−μ3mg=m(a+2)(2)
From equation (1):
F=ma+μmg
Substituting this expression for F into equation (2):
ma+μmg−μ3mg=m(a+2)
Rearranging the equation gives:
ma+μmg−μ3mg=ma+2m
Subtracting ma from both sides:
μmg−μ3mg=2m
Factoring out mg:
mg(μ−μ3)=2m
This simplifies to:
mg(2μ3)=2m
Dividing both sides by m (assuming m≠0):
g(2μ3)=2
Multiplying both sides by 32g:
μ=2⋅32g=3g
The value of μ is:
μ=3g
Topper's Solved these Questions
Similar Questions
A force of 98N is just able to move a body of weight 45kg on a rough horizontal surface What are the coefficient of friction and angle of friction ? .
View SolutionA horizontal force of 129.4 N is applied on a 10 kg block which rests on a horizontal surface. If the coefficient of friction is 0.3, the acceleration should be
View Solution
Knowledge Check
- Question 1 - Select One
A horizontal force is applied on a body on a rough horizontal surface produces an acceleration ‘a’. If coefficient of friction between the body and surface which is μ is reduced to μ/3, the acceleration increases by 2 units. The value of 'μ' is
A2/3gB3/2gC3/gD1/g - Question 2 - Select One
A body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
Aμ=p22gm2xBμ=p22mgxCμ=p2mgxDμ=p2gm2x - Question 3 - Select One
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of these
A body of mass 2 kg is placed on rough horizontal plane. The coefficient of friction between body and plane is 0.2 Then,
 View Solution
View SolutionA block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
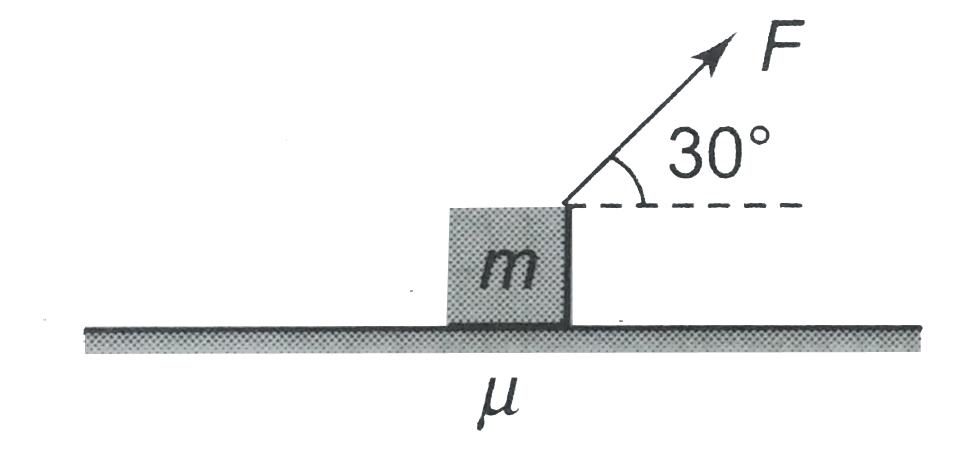 View Solution
View SolutionA body moves on a horizontal circular road of radius of r, with a tangential acceleration aT. Coefficient of friction between the body and road surface is μ. It begin to slip when it's speed is v, then :
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 View Solution
View Solution

