A small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

5
7
9
11
The correct Answer is:C
Vertical component of velocity of the ball do not change after collision.
Topper's Solved these Questions
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Subjective type Questions
9 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-I (H.W)
52 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Multiple Answer
11 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
Similar Questions
Two large rigid vertical walls A and B are parallel to each other and separated by 10m. A particle of mass 10g is projected with an initial velocity of 20m/s at 45∘ to the horizontal from point P on the ground, such that AP=5m. The plane of motion of the particle is vertical and perpendicular to the walls. Assuming that all the collisions are perfectly elastic, find the maximum height attained by the particle and the total number of collisions suffered by the particle with the walls before it hits ground. Take g=10m/s2.

View SolutionIn the previous problem , if the collision is head - on elastic , find (a) the velocities of balls immediately after the collision and (b) the maximum height attained by eacl ball.
View Solution
Knowledge Check
Suppose a ball is projected with speed u at an angle α with horizontal. It collides at some distance with a wall parallel to y-axis.
Let vx and vy be the components of its velocity along x and y-directions at the time of impact with wall. Coefficient of restitution between the ball and the wall is e. Component of its velocity along y-diection (common tangent) vy will remain unchanged while component of its velocity along x -direction (common normal) vx will become evx is opposite direction.
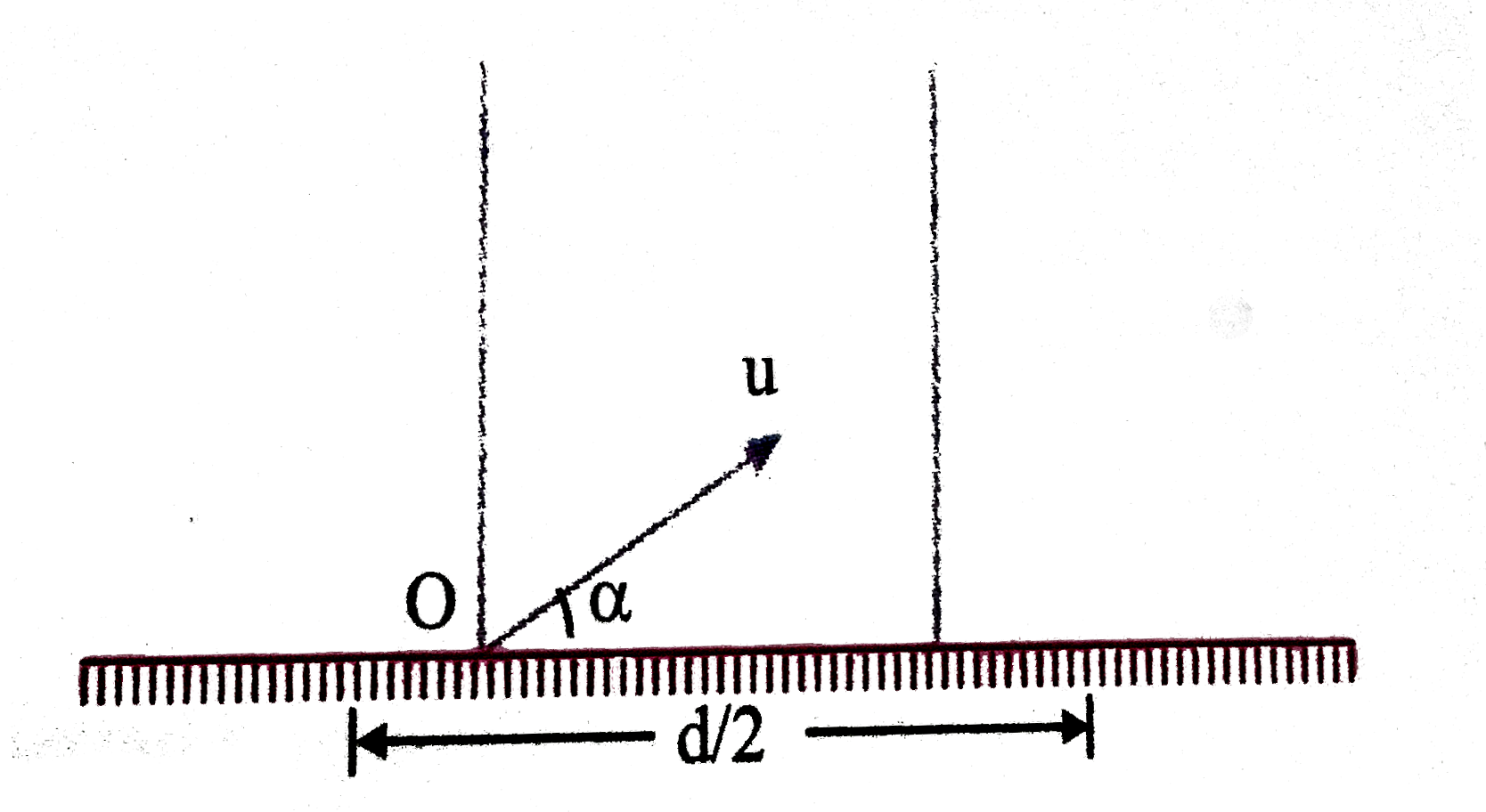
The situation shown in the figure a small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic (for first and second problems), the walls are supposed to be very tall.
The total time taken by the ball to come back to the ground (if collision is inelastic) isA>2usinαgB<2usinαgC=2usinαgD=2ucosαgTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
A−20ms−1B−5ms−1C1.0ms−1D−10ms−1
A small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View SolutionA ball is projected with velocity v0 at an angle α to the horizonal, towards a smooth wall which appraches the ball. With velocity u. After collision the ball retraces its path to the point of projection . What is the time t taken by the ball form the instant of projection to point of impact ?

View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n/2. All surfaces are smooth. Find the value of n.

View SolutionIn an elastic collision between smooth balls :
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View Solution
