A uniform rod of mass 2kg and length l is lying on a horizontal surface. If the work done in raising one end of the rod through an angle 45∘ is 'W', then the work done in raising it further 45∘ is
W
√2W
W√2
(√2−1)W
The correct Answer is:D
To solve the problem, we need to calculate the work done in raising one end of a uniform rod further after it has already been raised through an angle of 45∘.
1. Understanding the Initial Setup:
- We have a uniform rod of mass m=2kg and length l lying horizontally.
- The center of mass of the rod is located at a distance of l2 from either end.
2. Work Done in Raising the Rod to 45∘:
- When one end of the rod is raised to an angle of 45∘, the height of the center of mass (h1) can be calculated using trigonometry.
- The height h1 when the rod is at 45∘ is given by:
h1=l2sin(45∘)=l2⋅1√2=l2√2
- The work done W in raising the rod to this position against gravity is:
W=mgh1=mg⋅l2√2=2g⋅l2√2=gl√2
3. Raising the Rod from 45∘ to 90∘:
- Now we need to calculate the work done W′ in raising the rod from 45∘ to 90∘.
- The height h2 when the rod is vertical (at 90∘) is:
h2=l2
- The work done W′ in raising the rod from 45∘ to 90∘ is:
W′=mgh2=mg⋅l2=2g⋅l2=gl
4. Finding the Relationship Between W′ and W:
- Now we can express W′ in terms of W:
W′=mgh2=mg⋅l2=2g⋅l2=gl
- From the previous calculation, we have:
W=gl√2
- Therefore, the ratio of W′ to W is:
W′W=glgl√2=√2
- Thus, we can express W′ as:
W′=W⋅√2
Final Answer:
The work done in raising the rod further from 45∘ to 90∘ is:
W′=W⋅√2
- We have a uniform rod of mass m=2kg and length l lying horizontally.
- The center of mass of the rod is located at a distance of l2 from either end.
- When one end of the rod is raised to an angle of 45∘, the height of the center of mass (h1) can be calculated using trigonometry.
- The height h1 when the rod is at 45∘ is given by:
h1=l2sin(45∘)=l2⋅1√2=l2√2
- The work done W in raising the rod to this position against gravity is:
W=mgh1=mg⋅l2√2=2g⋅l2√2=gl√2
- Now we need to calculate the work done W′ in raising the rod from 45∘ to 90∘.
- The height h2 when the rod is vertical (at 90∘) is:
h2=l2
- The work done W′ in raising the rod from 45∘ to 90∘ is:
W′=mgh2=mg⋅l2=2g⋅l2=gl
- Now we can express W′ in terms of W:
W′=mgh2=mg⋅l2=2g⋅l2=gl
- From the previous calculation, we have:
W=gl√2
- Therefore, the ratio of W′ to W is:
W′W=glgl√2=√2
- Thus, we can express W′ as:
W′=W⋅√2
The work done in raising the rod further from 45∘ to 90∘ is:
W′=W⋅√2
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angular velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View Solution
Knowledge Check
A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
AmglBmgl/2Cmgl4D2mglA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpmlA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 A2πmlPBπml3PCπml12PD2πml3P
A2πmlPBπml3PCπml12PD2πml3P
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
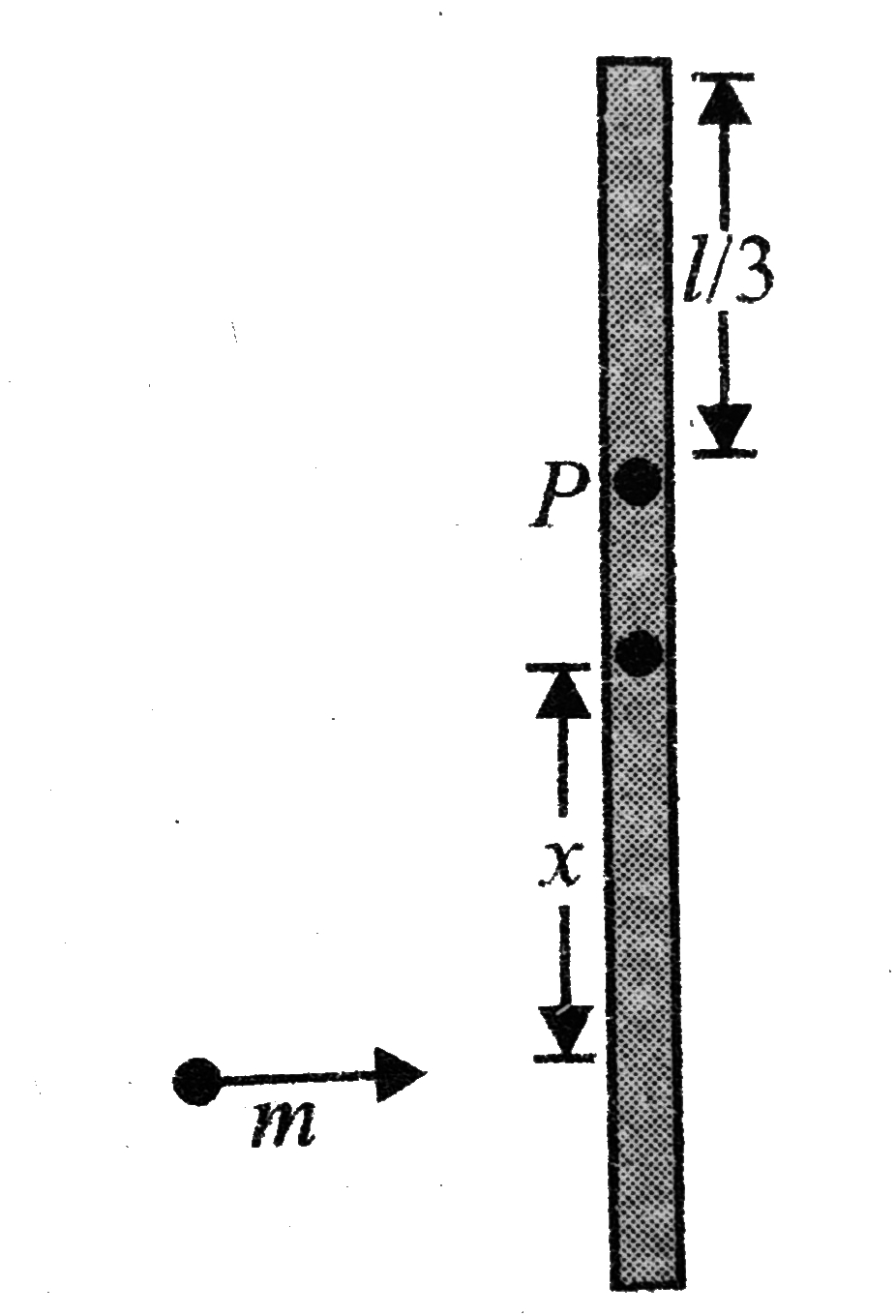
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘
View SolutionA metre scale of mass 200 g, is lying on a horizontal table. What is the work done by student in making it stand vertically on one of its ends?
View Solution