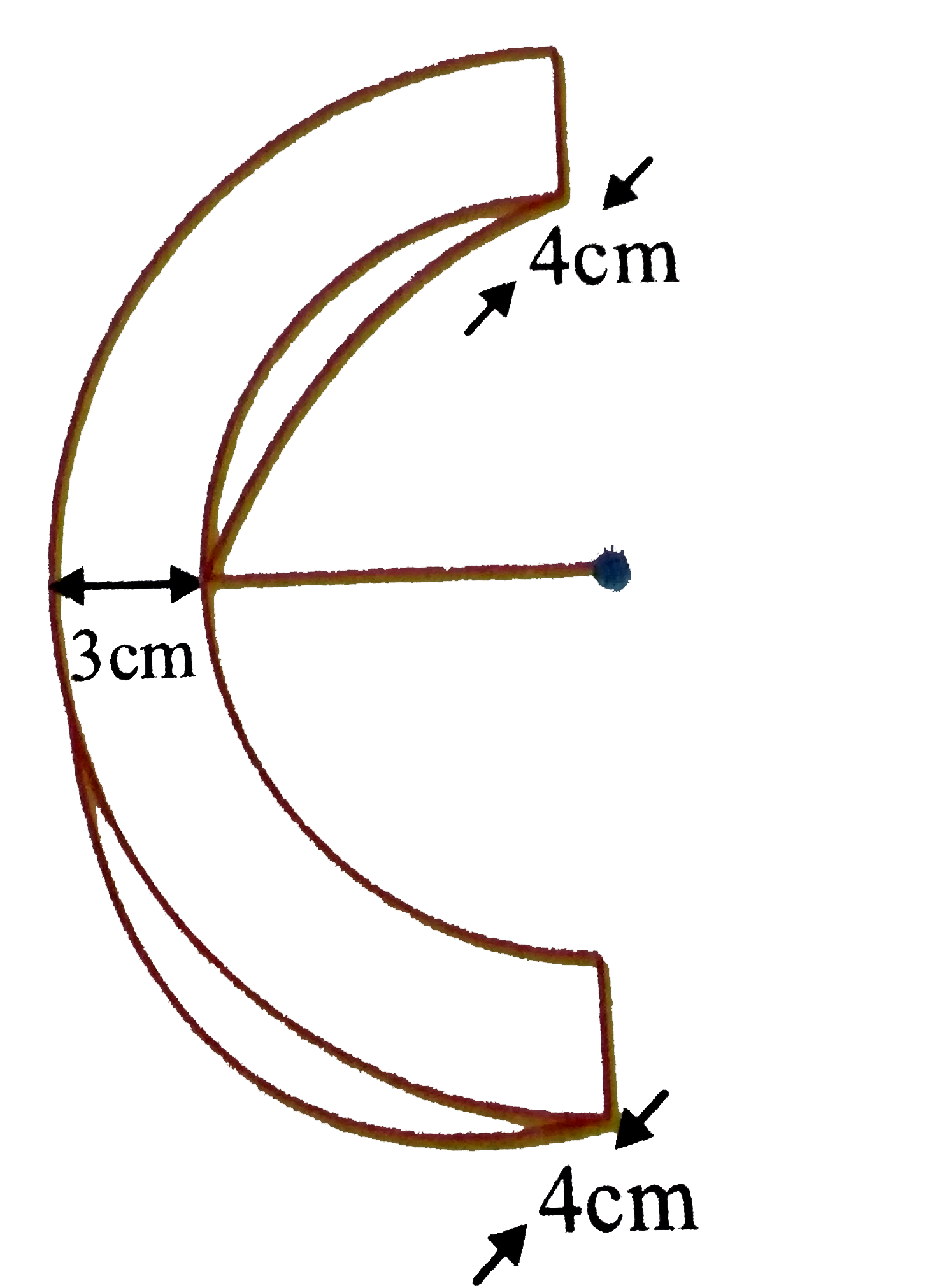
The resistance of a semicircle shown in fig. Between its two end faces is (Given that radial thickness $= 3 c m$ , axial thickness $= 4 c m$ , inner radius $= 6 c m$ and resistivity $= 4 \times 10^{- 6} Ω c m$ )

A

$24.15 \times 10^{- 6} Ω$

B

$7.85 \times 10^{- 7} Ω$

C

$7.85 \times 10^{- 6} Ω$

D

$7.85 \times 10^{- 5} Ω$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Here, $A = 4 c m \times 3 c m = 12 c m^{2}$
$l = π r = π (6 + \frac{3}{2}) = π \times 7.5 c m$
$R = \frac{ρ l}{A} = \frac{4 \times 10^{- 6} \times π \times 7.5}{12}$
$= 7.85 \times 10^{- 6} o h m$ .

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The volume of metallic cylindrical pipe is $748 c m^{3} .$ Its length is 14cm and its external radius is 9cm. Find its thickness.
A $1.5$ cm
B $0.5$ cm
C2 cm
D1 cm
Question 2 - Select One
The volume of a metallic cylindrical pipe is $784 c m^{3}$ . Its length is 14 cm and its external radius is 9 cm. Find its thickness
A1 cm
B2 cm
C81 cm
D17 cm
Question 3 - Select One
What is the volume of a hollow cylinder open at both ends, if its length is 25 cm, external radius is 10 cm and thickness is 1 cm ?
(Take $π = \frac{22}{7}$ )
A2985.72 cu. Cm
B746.43 cu. cm
C2239.29 cu. cm
D1492.86 cu. cm

NARAYNA-CURRENT ELECTRICITY-Level 3

Home
Ask Doubt
Profile