Activation energy (Ea) and rate constants (k1 and k2) of a chemical reaction at two different temperatures (T1 and T2) are related by
Ink2k1=EaR(1T1−1T2)
Ink2k1=−EaR(1T1−1T2)
Ink2k1=−Ea2.303R(1T2−1T1)
Ink2k1=−EaR(1T2+1T1)
The correct Answer is:A
Rate constants for most chemical reactions closely follow Arrhenius equation:
k=Ae−Ea/RT
Taking the natural logarithm of both sides of the Arrhenius equation gives
Ink=InA−Ea/RT
Now we write equation for two different absolute temperatures T1 and T2 . We write K1 for the rate constant at temperature T1 and K2 for the constant at temperature T2 .
InK2=InA−EaRT2
InK2=InA−EaRT1
Here we assume that the activation energy Ea and the frequency factor A do not vary with temperature.
We eliminate In A by subtracting the equations.
Ink2−InK1=−EaRT2+EaRT11
or Ink2k1=EaR(1T1−1T2)
Topper's Solved these Questions
- CHEMICAL KINETICSBook:R SHARMAChapter:CHEMICAL KINETICSExercise:Question Bank (Building the knowledge)
Explore 53 Videos
- BIOMOLECULESBook:R SHARMAChapter:BIOMOLECULESExercise:Archives
Explore 47 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:R SHARMAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:Archives
Explore 11 Videos
Similar Questions
The rate constants k1 and k2 of two reactions are in the ratio 2:1. The corresponding energies of acativation of the two reaction will be related by
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
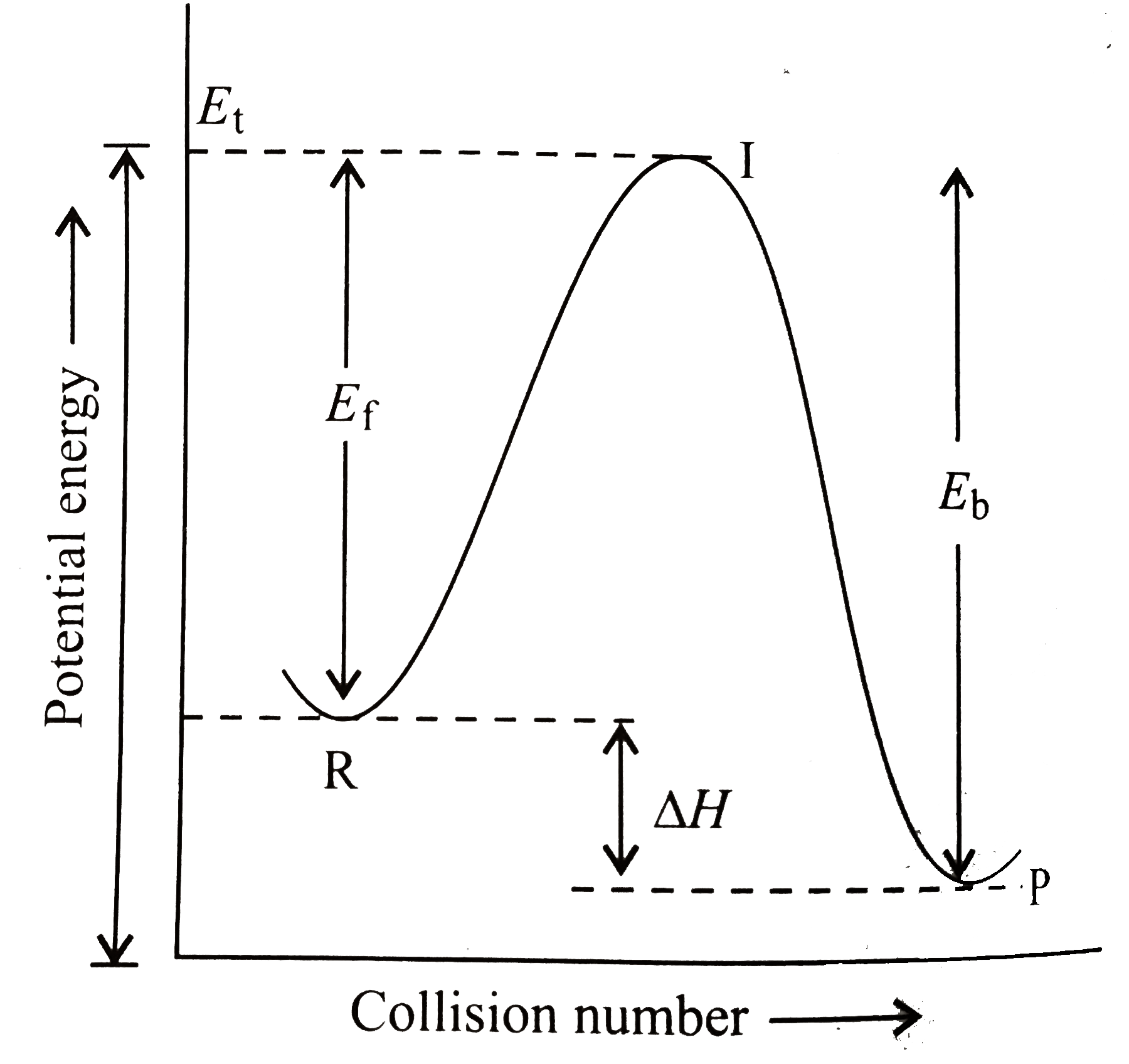
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View Solution
Knowledge Check
Activation energy (Ea) and rate constant (k1andk2) of chemical reaction at two different temperatures (T1andT2) are related by :
AInk2k1=EaR[1T1−1T2]BInk2k1=EaR[1T2−1T1]CInk2k1=EaR[1T2+1T1]DInk2k1=EaR[1T1+1T2]Activation energy (Ea) and rate constant (K1 and (K2) for a chemical reaction at two different temperatures T1 and T2 are related by:
AIn K2K1=EaR(1T1−1T2)BIn k2k1=−EaR(1T2−1T1)CIn k2k1=−EaR(1T2+1T1)DIn k2k1=EaR(1T1−1T2)Activation energy (Ea) and rate constants (k1andk2) of a chemical reaction at two different temperature (T1andT2) are related by
AIn k2k1=−EaR(1T1−1T2)BIn k2k1=−EaR(1T2−1T1)CIn k2k1=−EaR(1T2+1T1)DIn k2k1=EaR(1T1−1T2)
The rate constant K1 of a reaction is found to be double that of rate constant K2 of another reaction. The relationship between corresponding activation energies of the two reaction at same temperature (E1andE2) can be represented as:
View SolutionTwo reaction : X→ Products and Y→ Products have rate constants k1 and k2 at temperature T and activation energies E1 and E2, respectively. If k1>k2 and E1<E2 (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in k2 will be greater than increaisng in k1.
(II) On increaisng the temperature, increase in k1 will be greater than increase in k2.
(III) At higher temperature, k1 will be closer to k2.
(IV) At lower temperature, k1<k2
View SolutionTwo reactions having their energy of activation E1 and E2 temperature coefficients Tc1 and Tc2 respectively within the temperature 300 and 310K. The ratio of their temperature coefficient is:
View SolutionThe activation energies of two reactions are E1 & E2 with E1>E2. If temperature of reacting system is increased from T1 (rate constant are k1 and k2) to T2 (rate constant are k11 and k12) predict which of the following alternative is incorrect.
View SolutionTwo reactions A→ products and B→ products have rate constants ka and kb respectively at temperature T and activation energies are Ea and Eb respectively.
If ka>kb and Ea<Eb and assuming the freuency factor A in both the reactions are same then
View Solution