In the figure, the radius of the larger circle is 2 cm and the radius of the smaller circle is 1 cm and the larger circle passes through the centre of the smaller circleThe length (in cm) of the chord AB is :
Step by step video & image solution for In the figure, the radius of the larger circle is 2 cm and the radius of the smaller circle is 1 cm and the larger circle passes through the centre of the smaller circleThe length (in cm) of the chord AB is : by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
In the figure, the radius of the larger circle is 2 cm and the radius of the smaller circle is 1 cm and the larger circle passes through the centre of the smaller circleThe length (in cm) of the chord AB is :
View SolutionThe adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between two circles ( π=3.14)
View Solution
Knowledge Check
In the figure below, the radius of the bigger circle is (√2+1) cm and the radius of all the smaller circles are equal. Each of the smaller circles touches two of the other three smaller circles and the larger circle as shown. Find the area (in cm2) of the shaded portion.
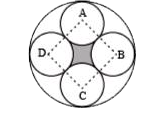A2−π2B1Cπ/4DCannot to determinedIn the given figure there are 3 semicircles , the radii of each smaller circle is equal. If the radius of the larger circle be 22 cm , then the area of the shaded region is :
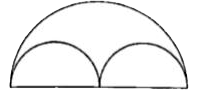A363π4B363π3C236.5πD363πThe radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
A24 cmB12 cmC30 cmD18 cm
In the given figure,diameter of larger semi-circle is 14 cm and radius of smaller semi-circle is 3.5cm. find :
View SolutionIn the adjoining figure the diameter of the larger circle is 10 cm and the smaller circle touches internally the lager circle at P and passes through O, the center of the larger circle, Chord SP cuts the smaller circle at R and OR is equal to 4 cm. What is the length of the chord SP ?
View SolutionIn two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View Solution