Consider the graph of y=x2. Let A be a point on the graph in the first quadrant. Let B be the intersection point of the tangent on y=x2 at the point A and the x-axis. If the area of the figure surrounded by the graph of y=x2 and the segment OA is (pq) times as large as the area of the triangle OAB (where O is origin), then find the least value of (p+q) where p,q∈N.
Step by step video & image solution for Consider the graph of y=x^2. Let A be a point on the graph in the first quadrant. Let B be the intersection point of the tangent on y=x^2 at the point A and the x-axis. If the area of the figure surrounded by the graph of y=x^2 and the segment OA is (p/q) times as large as the area of the triangle OAB (where O is origin), then find the least value of (p+q) where p, q in N. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let B and C are points of interection of the parabola y=x2 and the circle x2+(y−2)2=8. The area of the triangle OBC, where O is the origin, is
A2B4C6D8The point (2,−1) on the graph y=f(x) is shifted to which point on the graph of y=f(x+2)?
A(4,1)B(4,−1)C(0,−1)D(0,−3)At figure shows the graph of y=a−x2 fro some constant a. If the square ABCD intersects the graph at point A and B and the area of the square is 16, what is the value of a?
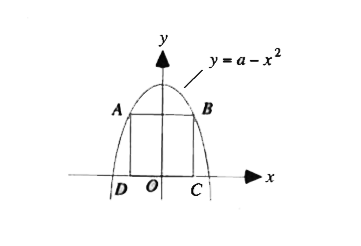 A2B4C6D8
A2B4C6D8
Let B and C are points of interection of the parabola y=x2 and the circle x2+(y−2)2=8. The area of the triangle OBC, where O is the origin, is
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
View Solution
