If two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
To prove that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle, we can follow these steps:
1. Identify the Setup:
Let the two parallel lines be AB and CD, and let the transversal be EF intersecting AB at point G and CD at point H.
2. Label the Angles:
The angles formed at the intersection points are:
- ∠BGH and ∠AGH (interior angles on the same side of the transversal)
- ∠DHG and ∠CHG (the other pair of interior angles on the same side of the transversal)
3. Angle Relationships:
Since AB∥CD and EF is a transversal, we know:
∠BGH+∠GHD=180∘
This can be labeled as Equation (1).
4. Bisectors of the Angles:
Let GL be the bisector of ∠BGH and GM be the bisector of ∠AGH. Similarly, let HL be the bisector of ∠DHG and HM be the bisector of ∠CHG.
5. Establishing Equal Angles:
Since GL and GM are angle bisectors:
∠BGL=∠AGH=12∠BGH
∠GHM=∠AGH=12∠AGH
6. Using the Sum of Angles:
From Equation (1), we multiply by 12:
12(∠BGH+∠GHD)=90∘
Thus, we can say:
∠BGL+∠GHM=90∘
7. Triangles and Angles:
In triangle GHL:
∠GHL+∠GLH+∠HGL=180∘
Substituting ∠GHL=90∘:
90∘+∠GLH+∠HGL=180∘
Therefore, ∠GLH=90∘.
8. Establishing Parallel Lines:
Since ∠BGL=∠AGH and ∠GHM=∠DHG, we have:
GL∥HMandHL∥GM
9. Conclusion:
Since both pairs of opposite sides are parallel and one angle is 90∘, quadrilateral GLMH is a rectangle.
Final Statement:
Thus, we have proved that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle.
---
Let the two parallel lines be AB and CD, and let the transversal be EF intersecting AB at point G and CD at point H.
The angles formed at the intersection points are:
- ∠BGH and ∠AGH (interior angles on the same side of the transversal)
- ∠DHG and ∠CHG (the other pair of interior angles on the same side of the transversal)
Since AB∥CD and EF is a transversal, we know:
∠BGH+∠GHD=180∘
This can be labeled as Equation (1).
Let GL be the bisector of ∠BGH and GM be the bisector of ∠AGH. Similarly, let HL be the bisector of ∠DHG and HM be the bisector of ∠CHG.
Since GL and GM are angle bisectors:
∠BGL=∠AGH=12∠BGH
∠GHM=∠AGH=12∠AGH
From Equation (1), we multiply by 12:
12(∠BGH+∠GHD)=90∘
Thus, we can say:
∠BGL+∠GHM=90∘
In triangle GHL:
∠GHL+∠GLH+∠HGL=180∘
Substituting ∠GHL=90∘:
90∘+∠GLH+∠HGL=180∘
Therefore, ∠GLH=90∘.
Since ∠BGL=∠AGH and ∠GHM=∠DHG, we have:
GL∥HMandHL∥GM
Since both pairs of opposite sides are parallel and one angle is 90∘, quadrilateral GLMH is a rectangle.
Thus, we have proved that the bisectors of the two pairs of interior angles formed by two parallel lines intersected by a transversal enclose a rectangle.
Similar Questions
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View Solution
Knowledge Check
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
A1B2C3D4Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
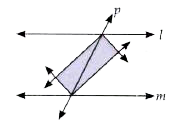 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
If two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines intersected by a transversal , then name the pair of angles formed that are equal .
View Solution
