If two angles of a triangle are equal;then sides opposite to them are also equal.
To prove that if two angles of a triangle are equal, then the sides opposite to them are also equal, we can follow these steps:
1. Identify the Triangle and Angles:
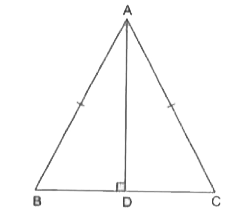
Let triangle ABC be given, where angle A is equal to angle B (∠A = ∠B).
2. Draw the Angle Bisector:
From point A, draw a line segment AD that bisects angle A. This means that angle BAD is equal to angle CAD (∠BAD = ∠CAD).
3. Label the Angles:
Let angle ABD be equal to angle ACD (∠ABD = ∠ACD). This is given in the problem.
4. Identify the Common Side:
The line segment AD is common to both triangles ABD and ACD.
5. Establish Triangle Congruence:
Now we have:
- ∠BAD = ∠CAD (from the angle bisector)
- ∠ABD = ∠ACD (given)
- AD is common to both triangles.
This gives us two angles and the included side for both triangles. Therefore, we can use the Angle-Angle-Side (AAS) congruence criterion.
6. Conclude Triangle Congruence:
By AAS, triangle ABD is congruent to triangle ACD (ΔABD ≅ ΔACD).
7. State the Result:
Since the triangles are congruent, the sides opposite the equal angles must also be equal. Thus, we have:
AB = AC.
Final Conclusion:
If two angles of a triangle are equal, then the sides opposite to them are also equal.
---
Let triangle ABC be given, where angle A is equal to angle B (∠A = ∠B).
From point A, draw a line segment AD that bisects angle A. This means that angle BAD is equal to angle CAD (∠BAD = ∠CAD).
Let angle ABD be equal to angle ACD (∠ABD = ∠ACD). This is given in the problem.
The line segment AD is common to both triangles ABD and ACD.
Now we have:
- ∠BAD = ∠CAD (from the angle bisector)
- ∠ABD = ∠ACD (given)
- AD is common to both triangles.
By AAS, triangle ABD is congruent to triangle ACD (ΔABD ≅ ΔACD).
Since the triangles are congruent, the sides opposite the equal angles must also be equal. Thus, we have:
AB = AC.
If two angles of a triangle are equal, then the sides opposite to them are also equal.
Similar Questions
Test the validity of the following argument :
S1 : If two sides of a triangles are equal, then the opposite angles are equal.
S2 : Two sides of a triangle are not equal
S : Two opposite angles are not equal.
View SolutionWhich of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.
View Solution
Knowledge Check
If the area(!) and an angle(θ) of a triangle are given , when the side opposite to the given angle is minimum , then the length of the remaining two sides are
A√2!sinθ,√3!sinθB√2!sinθ,√2!sinθC√4!sinθ,√4!sinθD√6!sinθ,√6!sinθIf one angle of a triangle is equal to half the sum of the other two equal angles, then the triangle is :
AisoscelesBscaleneCequilateralDright angledConsider the following statements :
(1) If three sides of a triangle are equal to three sides of another triangle, then the triangles are congruent.
(2) If three angles of a triangles are equal to three angles of another triangle respectively, then the two triangles are congruent. Of these statements :A1 is correct and 2 is falseBboth 1 and 2 are falseCboth 1 and 2 are correctD1 is false and 2 is correct
If two angles of a triangle are unequal , then the smaller angle has the ________ side opposite to it .
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf two sides of a triangle are unequal; the longer side has greater angle opposite to it.
View SolutionShow that in an isosceles triangle, the angles opposite to the equal sides are equal.
View SolutionOne of the exterior angles of a triangle is 800 , and the interior opposite angles are equal to each other. What is the measures of each of these two angles?
View Solution
