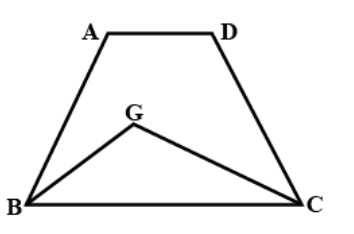
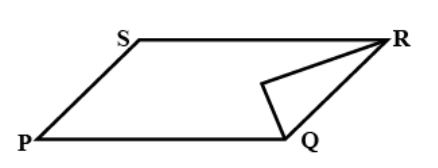
Which of the following figures lie on the same base and between the same parallels. In such a case; write the common base and two parallels :
To solve the question of identifying which figures lie on the same base and between the same parallels, we can follow these steps:
Step 1: Identify the Figures
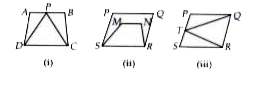
We have three figures to analyze:
1. Trapezium ABCD and triangle PDC
2. Parallelogram PQRS and trapezium MNSR
3. Parallelogram PQSR and triangle TQR
Step 2: Analyze Each Figure
Figure 1: Trapezium ABCD and Triangle PDC
- Identify the parallel sides: AB is parallel to DC.
- Common base: DC.
- Since triangle PDC lies on base DC and between the parallels AB and DC, this figure satisfies the condition.
Figure 2: Parallelogram PQRS and Trapezium MNSR
- Identify the parallel sides: PQ is parallel to SR (as PQRS is a parallelogram).
- Check if MN lies on the same base: MN does not lie on PQ or SR.
- Since MN does not connect with PQ, this figure does not satisfy the condition.
Figure 3: Parallelogram PQSR and Triangle TQR
- Identify the parallel sides: PS is parallel to QR (as PQSR is a parallelogram).
- Common base: QR.
- Triangle TQR lies on base QR and between the parallels PS and QR, satisfying the condition.
Step 3: Conclusion
The figures that lie on the same base and between the same parallels are:
- Figure 1: Trapezium ABCD and Triangle PDC (Common base: DC, Parallels: AB and DC)
- Figure 3: Parallelogram PQSR and Triangle TQR (Common base: QR, Parallels: PS and QR)
Final Answer
The figures that lie on the same base and between the same parallels are:
1. Trapezium ABCD and Triangle PDC
2. Parallelogram PQSR and Triangle TQR
We have three figures to analyze:
1. Trapezium ABCD and triangle PDC
2. Parallelogram PQRS and trapezium MNSR
3. Parallelogram PQSR and triangle TQR
Figure 1: Trapezium ABCD and Triangle PDC
- Identify the parallel sides: AB is parallel to DC.
- Common base: DC.
- Since triangle PDC lies on base DC and between the parallels AB and DC, this figure satisfies the condition.
- Identify the parallel sides: PQ is parallel to SR (as PQRS is a parallelogram).
- Check if MN lies on the same base: MN does not lie on PQ or SR.
- Since MN does not connect with PQ, this figure does not satisfy the condition.
- Identify the parallel sides: PS is parallel to QR (as PQSR is a parallelogram).
- Common base: QR.
- Triangle TQR lies on base QR and between the parallels PS and QR, satisfying the condition.
The figures that lie on the same base and between the same parallels are:
- Figure 1: Trapezium ABCD and Triangle PDC (Common base: DC, Parallels: AB and DC)
- Figure 3: Parallelogram PQSR and Triangle TQR (Common base: QR, Parallels: PS and QR)
The figures that lie on the same base and between the same parallels are:
1. Trapezium ABCD and Triangle PDC
2. Parallelogram PQSR and Triangle TQR
Similar Questions
Which of the following figures lie on the same base and between the same parallels.In such a case, write the common base and the two parallels.
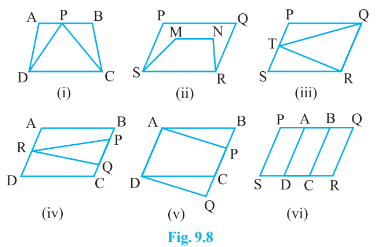
View SolutionWhich of the following figure lie in the same base and between the same parallels. In such a case, write the common base and the two parallels.
View Solution
Knowledge Check
In which of the following figures, you find two polygons on the same base and between the same parallels?
ABCD
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

View SolutionWhich of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

View SolutionFigures on the same base and between the same parallels
View SolutionOut of the following given figures, which are on the same base but not between the same parallels?
View SolutionTriangles on the same base and between the same parallel are equal in area.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View SolutionA ||gm and a rectangle on the same base and between the same parallels are equal in area
View Solution