Question

Cuboid

Explanation

Cuboid

In this chapter, you would be able to get the best idea on cuboid as well as cuboid formula volume. We would also include the study of the surface area of a cuboid. To make things clearer, we will work on some solved problems.

What is cuboid?

A cuboid is a three-dimensional shape that consists of eight vertices, six faces, and twelve edges. In other words, it is a polyhedron where the faces of the cuboid are parallel as well as equal in dimensions. Compared to the cube and cylinders, the area and volume differ.

What is the shape of a cuboid?

A cuboid is bounded by six rectangular plane reasons which are a closed 3-dimensional geometrical figure.

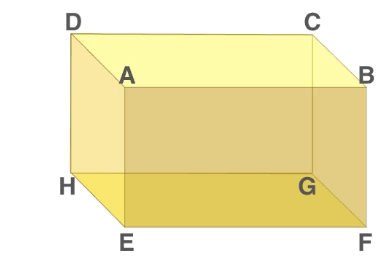
Cuboid formula

Have a look at the cuboid below where the breadth is ‘b’ cm, length be ‘l’ cm and height be ‘h’ cm.

So, here,

Area of face BFGC = Area of face AEHD = (b ×h) cm²

Area of face EFGH = Area of Face ABCD = (l× b) cm²

Area of face DHGC = Area of face ABFE = (l ×h) cm²

Here, Total surface area of a cuboid = Sum of the areas of all its 6 rectangular faces

In other words, Total Surface Area of a Cuboid = 2 (lb + bh + lh )

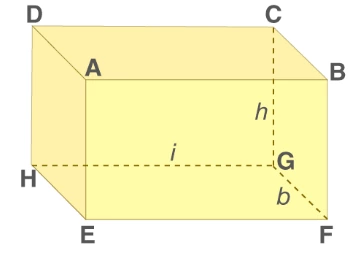
Lateral surface area of a Cuboid

The lateral surface area of a solid is the sum of surface areas of all sides except the top and bottom face of solid

Let us consider a Cuboid of length to be ‘l’, breadth to be ‘b’ and height to be ‘h’.

Now, the lateral surface area of the cuboid= Area of face ADHE + Area of face ABFE + Area of face BCGF + Area of face DCGH

=2 (b × h) + 2 (l × h)

=2h (l + b)

So Lateral Surface of a Cuboid = 2h ( l + b )

Volume of Cuboid

The cuboid volume is equal to the product of the area of one surface and height.

So, Volume of the Cuboid = ( l x b x h) cubic units.

Diagonal of cuboid

It is important to note that the length of diagonal of the cuboid is √( l² + b² +h²)

Perimeter of Cuboid

It on the basis of the length, width and height, that the perimeter of the cuboid is calculated.  The value of the edges is different because the cuboid has 12 edges. So, the perimeter is:

Perimeter of a cuboid = 4 (l + b + h)

Here, l, b and h are length, breadth and height, respectively.

Now, we will summarize all the formulas in the table below:

Formulas	Cuboid
Surface Area	2(lb + bh +lh)
Lateral Surface Area	2h(l +b)
Volume	l × b × h
Diagonal Length	√( l2 + b2 +h2)
Perimeter	4 (l + b + h)

Related Videos:

• Volume of a cuboid


• Surface area of a cuboid


• Cube and Solid cube


• Lateral surface area of a cuboid


• Surface area of cube


• Lateral surface area of cube

We will now proceed further to solve different problems on cuboid to get a clear understanding of it.

Problem 1: A cuboid has dimensions of 3 inches × 4 inches × 4 inches. Find the total surface area?

Solution:  Here,

Length = 3 inches

Breadth = 4 inches

Height = 4 inches

We know that the total Surface Area (TSA) = 2 (lb + bh + hl )

TSA = 2 (3 ×4 + 4 × 7 + 4 × 3)

TSA = 2 (12 + 28 + 12)

TSA = 104

So, we find that the total surface area of this cuboid is 104 inches²

Problem 2: A cuboid has dimensions of 4 inches × 5 inches × 7 inches. Calculate the total surface area?

Solution:  Here,

Length = 4 inches

Breadth = 5 inches

Height = 7 inches

We know that the total Surface Area (TSA) = 2 (lb + bh + hl )

TSA = 2 (4 × 5 + 5 × 7 + 7 × 4)

TSA = 2 (20 + 35 + 28)

TSA = 166

So, we find that the total surface area of this cuboid is 166 inches²

Problem 3:  The length, width and height of a cuboid are 10 cm, 12 cm and 15 cm respectively. Find the lateral surface area of the cuboid?

Solution: Given,

Length = 10 cm

Breadth = 12 cm

Height = 15 cm

As we know

Lateral surface area of a cuboid is:

LSA = 2h ( l + w )

So, LSA = 2 × 15 (10 + 12)

LSA = 660 cm²

Problem 4: A cube has its sides equal to 4 cm in length. Find the surface area of it.

Solution: Given length, ‘a’= 4 cm

Surface area of the cube = 6a²

= 6× 4² 

= 6 ×16

= 96 cm²

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 9 Chapter Surface Area And Volume