Cube and Solid cube
Cube
When we say cube in Maths or in Geometry, it is a solid 3-dimensional figure. It has got 12 edges, 8 vertices and 6 square faces. Here, we will discuss the properties of the cube, surface area of a cube, volume of a cube along with some important examples. These examples would help to provide you with a good and clear idea on how to come up with the right solution by using the correct methods. It is important to know that the other solid shapes are cylinder, cuboid, sphere and cone.
Properties of Cube
Let’s try to understand the properties of the cube as below:
- All its faces are in the shape of a square.
- There are equal dimensions in all the faces or sides.
- The three faces and three edges are met by each of the vertices.
- The edges opposite to each other are always parallel.
- Each of the faces meets the other four faces.
- The plane angles of the cube which are found are the right angle.
What is the surface area of Cube?
The surface area is the region which is occupied by it on a flat surface. The area occupied by it will be in the form of 3D plane. This is because a cube is a three-dimensional object. It has got six faces in a cube, and so calculating the surface area of the cube covered by each face is required.
Let us have a look at the cube below. We will call the length of one side ‘a’.
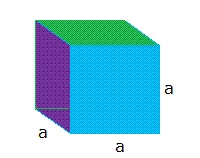
Basically, you need to use the following cube template when you wish to make a cube-like the one shown above.
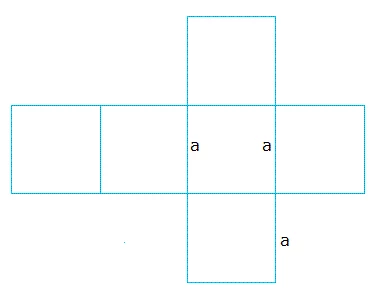
If you look at the cube template above, you will find six sides where each side is a square. Here, the length of an edge is ‘a’ for which the area of one square will be a x a = a2
Now, you can find that there are six sides, so the total surface area (SA) can be found as:
SA = a2 + a2 + a2 + a2 + a2 + a2
SA = 6 × a2
So, coming to the formula of the surface area of the cube, it is:
Surface Area of Cube = 6a2
We will look at an example to make you get a more clear idea about it so that you do not get confused at all.
Problem: The length of one side is 4 cm. Find out the surface area.
Solution:
Surface area = 6 × a2
Surface area = 6 × 42
Surface area = 6 × 4 × 4
Surface area = 6 × 16
Surface area = 96 cm2
Volume of Cube
Volume of a cube is the space that is contained in a cube. In order to understand the formula of the volume of cube formula, we need to concentrate on it in the best way. Let’s for example, the volume calculates the object if we need to immerse a cubical shape object in the water. Here, the formula of the volume is:
Volume of cube = a x a x a = a3
Related Videos:
- Surface area of cube
- Lateral surface area of cube
- Cuboid
- Volume of a cuboid
- Surface area of a cuboid
- Lateral surface area of a cuboid
Cube of a number
A cube of a number is a number that is multiplied three times by itself.
When a number is multiplied three times by itself, the product obtained is called the cube of a number.
For a given number n, we define, cube of n = n × n × n, denoted by n³. Let’s have a look at some of the examples below;
(i) 2³ = (2 × 2 × 2) = 8.
Thus, cube of 2 is 8.
(ii) 3³ = (3 × 3 × 3) = 27.
Thus, cube of 3 is 27.
(iii) 4 × 4 × 4 = 64, here 64 is the cube of 4.
(iv) 5 × 5 × 5 = 125, here 125 is the cube of 5.
Cubes of negative integer:
When it comes to the cube of a negative integer, it is always negative.
For example:
(-1)³ = (-1) × (-1) × (-1) = -1,
(-2)³ = (-2) × (-2) × (-2) = -8
(-3)³ = (-3) × (-3) × (-3) = -27, etc.
Cube of a rational number:
We have, (a/b) ³ = a/b × a/b × a/b = (a × a × a)/(b × b × b) = a³/b³
Hence, (a/b) ³ = a³/ b³
For example:
(i) (-2/3) ³ = (-2) ³/ 3³ = {(-2) × (-2) × (-2)}/(3 × 3 × 3) = -8/27
(ii) (3/5) ³ = 3³/5 ³ = (3 × 3 × 3)/(5 × 5 × 5) = 27/125
Examples:
Problem: Find the cube of each of the following:
(i) (-7) (ii) 1²/₃ (iii) 2.5
Solution:
(i) (-7)³
= (-7) × (-7) × (-7)
= -343
(ii) (1²/₃)³
= (5/3) ³
= 5³/3³
= (5 × 5 × 5)/(3 × 3 × 3)
= 125/27
(iii) (2.5)³
= (25/10)³
= (5/2)³
= 5³/3³
= (5× 5 × 5)/(3× 3× 3)
= 125/27
Important Chapters:


SA = 6 × a2
Surface area = 6 × 42
Surface area = 6 × 4 × 4
Surface area = 6 × 16
Surface area = 96 cm2
For a given number n, we define, cube of n = n × n × n, denoted by n³. Let’s have a look at some of the examples below;
Thus, cube of 2 is 8.
(ii) 3³ = (3 × 3 × 3) = 27.
Thus, cube of 3 is 27.
(iii) 4 × 4 × 4 = 64, here 64 is the cube of 4.
(iv) 5 × 5 × 5 = 125, here 125 is the cube of 5.
For example:
(-1)³ = (-1) × (-1) × (-1) = -1,
(-2)³ = (-2) × (-2) × (-2) = -8
(-3)³ = (-3) × (-3) × (-3) = -27, etc.
Hence, (a/b) ³ = a³/ b³
For example:
(i) (-2/3) ³ = (-2) ³/ 3³ = {(-2) × (-2) × (-2)}/(3 × 3 × 3) = -8/27
(ii) (3/5) ³ = 3³/5 ³ = (3 × 3 × 3)/(5 × 5 × 5) = 27/125
(i) (-7) (ii) 1²/₃ (iii) 2.5
Solution:
(i) (-7)³
= (-7) × (-7) × (-7)
= -343
(ii) (1²/₃)³
= (5/3) ³
= 5³/3³
= (5 × 5 × 5)/(3 × 3 × 3)
= 125/27
(iii) (2.5)³
= (25/10)³
= (5/2)³
= 5³/3³
= (5× 5 × 5)/(3× 3× 3)
= 125/27
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of the volume of a cube and a solid sphere is 363 : 49. The ratio of an edge of the cube and the radius of the sphere is (taking π=227)
A7:11B22:7C11:7D7:22 - Question 2 - Select One
A solid cube and a solid sphere both made of same material are completely submerged in water but to different depths. The sphere and the cube have same surface area. The buoyant force is–
AGreater for the cube than the sphereBGreater for the sphere than the cubeCSame for the sphere and the cubeDGreater for the object that is submerged deeper - Question 3 - Select One
A solid cube and a solid sphere of the same material have equal surface area. Both are at the same temperature 120∘C, then
ABoth the cube and the sphere cool down at the same rateBThe cube cools down faster than the sphereCThe sphere cools down faster than the cubeDWhichever is having mor mass will cool down faster
How many cubes of side 2 cm can be made from a solid cube of side 10 cm ?
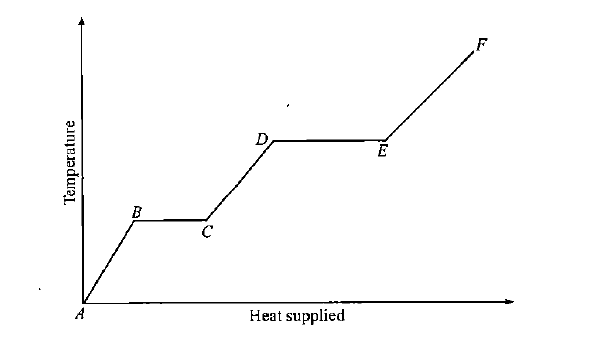
View SolutionA source of heat supplies heat at constant rate to a solid cube. The variatiion of the temperature of the cube with heat supplied is shown in figure. The portion DE of the graph represents conversion of
 View Solution
View SolutionA large right circular cone is made out of a solid cube edge 9 cm. Find the volume of the remaining solid.
View SolutionHow many smaller cubes of 1 cm side can be formed with a solid cube of 3 cm side ?
View SolutionA solid metallic cube of edge 4 cm is melted and recast into solid cubes of edge 1 cm. If x is the surface area of the melted cube and y is the total surface area of the cubes recast, then what is x:y ?
View Solution

