Question

What is Sphere ?

Explanation

Sphere

A sphere is a three-dimensional round object. Here, students will get an opportunity to learn a mathematical definition of a sphere, and discuss the formulas associated with spheres.

Definition of a Sphere

A sphere is a 3-dimensional geometrical figure that is completely round and circular - like a ball. Geometrically, a sphere is characterized as the arrangement of all points equidistant from a single point in space. The distance from an external point to the centre point of the sphere is the radius(r), and the longest straight line within a sphere is the diameter (d).

If you cut a sphere into two halves, you will obtain two hemispheres. It can be perceived as half of a sphere. The biggest circle of a sphere is a circle that has the same radius and centre as the sphere itself.

At the point when a circle changes into a sphere, no parameter such as radius or diameter, inside it changes. It just turns into a three-dimensional rendition of a planar circle. So a a sphere is a three-dimensional counterpart of a circle, with each point lying in space at equidistant from the fixed point or the inside, called the radius of that sphere.

Properties of Sphere

A sphere occupies the biggest space, but it has the smallest surface area. One can imagine that if something needs to be as small as possible and also have a large volume, it acquires the spherical shape. One such practical example is that of a balloon, which is round in shape, when you fill the air inside it. It holds maximum amount of air possible with the smallest amount of surface. There are other common examples such as the shape of water drops and bubbles.

Determining Surface Area of Sphere

To determine the surface area of any spherical thing, you need to measure the diameter of it.  Since the biggest circle in the sphere has same diameter and radius, so we deduce the diameter of the circle which will be equal to that of the sphere. A round ball of any sports is the good example of a sphere.

The total surface area of the sphere is equal to the area of four circles of same radius. It implies that the surface area of a sphere = 4 × Area of a circle = 4 × πr²

Surface Area of a Sphere = 4πr²

Determining Volume of a Sphere

Once can determine the volume of a spherical body through Archimedes principle. As per, Archimedes principle, when a solid body is immersed in a water-filled vessel, then the volume of water that floods out from the vessel is equivalent to the volume of that solid item, but following this principle is not feasible every time.

To deduce the formula/ expression for the volume of the sphere, we have to place a sphere/ball in a cylindrical vessel

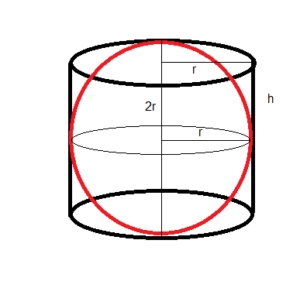
The above figure shows a sphere placed within a cylindrical vessel. The radius of the both circular bases of the cylinder is same as that of the radius of the sphere. The diameter of sphere is equal to the height of the container, since the sphere touches both bases of cylindrical vessel,

Assuming the volume of a spherical body to be 2/3rd of the cylindrical vessel, it implies:

Volume of sphere = 2/3  × Volume of Cylinder

We know Volume of Cylinder = 2/3   π r²h. 

Thus, we get, h = 2 r = 2/3 πr² (2r) = 4 / 3 πr³.

Hence, Volume of the Sphere = 4/3πr³