Find the Area of polygon
To find the area of a polygon given its vertices, we can use the method of dividing the polygon into triangles. Here’s a step-by-step solution to find the area of a polygon:
1. Identify the Vertices:
Let's say the vertices of the polygon are given as A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),…,N(xn,yn).
2. Determine the Number of Triangles:
For an n-sided polygon, you can divide it into n−2 triangles by drawing n−3 diagonals from one vertex.
3. Select a Vertex:
Choose one vertex as a reference point (for example, A) and connect it to all other non-adjacent vertices to form triangles.
4. Calculate the Area of Each Triangle:
Use the formula for the area of a triangle given its vertices (x1,y1),(x2,y2),(x3,y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Calculate the area for each triangle formed.
5. Sum the Areas:
Add the areas of all the triangles to get the total area of the polygon.
6. Final Result:
The total area calculated will be the area of the polygon.
Example:
Let's say we have a quadrilateral with vertices A(1,1),B(4,1),C(4,5),D(1,5).
1. Vertices: A(1,1),B(4,1),C(4,5),D(1,5)
2. Triangles: We can divide this quadrilateral into two triangles: ABC and ACD.
3. Area of Triangle ABC:
AreaABC=12|1(1−5)+4(5−1)+4(1−1)|=12|1(−4)+4(4)+4(0)|=12|−4+16|=12×12=6
4. Area of Triangle ACD:
AreaACD=12|1(1−5)+4(5−1)+1(1−1)|=12|1(−4)+1(0)+4(4)|=12|−4+16|=12×12=6
5. Total Area:
Total Area=AreaABC+AreaACD=6+6=12
Final Answer:
The area of the polygon is 12 square units.
Let's say the vertices of the polygon are given as A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),…,N(xn,yn).
For an n-sided polygon, you can divide it into n−2 triangles by drawing n−3 diagonals from one vertex.
Choose one vertex as a reference point (for example, A) and connect it to all other non-adjacent vertices to form triangles.
Use the formula for the area of a triangle given its vertices (x1,y1),(x2,y2),(x3,y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Calculate the area for each triangle formed.
Add the areas of all the triangles to get the total area of the polygon.
The total area calculated will be the area of the polygon.
Let's say we have a quadrilateral with vertices A(1,1),B(4,1),C(4,5),D(1,5).
2. Triangles: We can divide this quadrilateral into two triangles: ABC and ACD.
3. Area of Triangle ABC:
AreaABC=12|1(1−5)+4(5−1)+4(1−1)|=12|1(−4)+4(4)+4(0)|=12|−4+16|=12×12=6
4. Area of Triangle ACD:
AreaACD=12|1(1−5)+4(5−1)+1(1−1)|=12|1(−4)+1(0)+4(4)|=12|−4+16|=12×12=6
5. Total Area:
Total Area=AreaABC+AreaACD=6+6=12
The area of the polygon is 12 square units.
Similar Questions
Area of a polygon
View Solutionr-sided polygons are formed by joining the vertices of an n-sided polygon. Find the number of polygons that can be formed, none of whose sides coincide with those of the n-sided polygon.
View SolutionFind area of Polygon by Stair Method
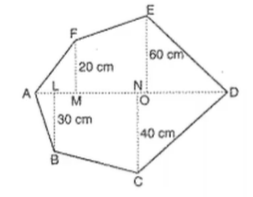
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionA regular polygon of 10 sides is constructed. Triangles are formed joining vertices of the polygon. Find the number of triangles
(i) if two sides of trinangle coincide with the sides of polygon.
(ii) if only one side of triangle coincide with the side of polygon.
View SolutionRegular polygon and its area
View SolutionFind the area of regular polygon of 7 sides whose each side measures 4 cm and circum-radius is 3 cm.(use √5=2.236)
View SolutionArea OF triangle ||Area OF polygon || Condition OF Collinearity OF 3 points
View SolutionA piece of paper is in the shape of a square of side 1m long. It is cut at the four corners to make a regular polygon of eight sides (octagon). The area of the polygon is
View SolutionA uniform wire of resistance R is shaped into a regular n sided polygon where n is even. Find the equivalent resistance between (i) opposite corners of polygon (ii) adjacent corners of polygon .
View Solution
