Area enclosed by two concentric circles
Step by step video & image solution for Area enclosed by two concentric circles by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
The area enclosed between two concentric circles is 770cm2 .If the radii of the circles differ by 7cm ,find both the radii.
View SolutionFind the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle, such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles. Find the radius of the third circle correct to one decimal place.
View Solution
Knowledge Check
The area of circle whose radius is 6 cm is trisected by two concentric circles. The radius of the smallest circle is
A2√3cmB2√6cmC2cmD3cmA chord of the larger among two concentric circles is of length 10 cm and it is tangent to the smaller circle. What is the area (in cm ) of the annular portion between the two circles?
A5π2B25πC5πD10πThe difference in the areas of two concentric circles is 66 cm2 and the radius of the outer circle is 11 cm. What is the radius of the inner circle?
A8 cmB9 cmC10 cmD7 cm
In Fig. 12.69, find the area of the shaded region, enclosed between two concentric circles of rade 7 cm and 14 cm where ∠AOC=40∘(Use π=227)
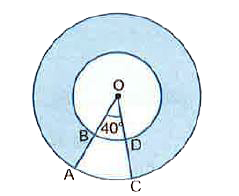
View SolutionThe area enclosed between the concentric circles is 770 cm2 . If the radius of the outer circle is 21 cm, find the radius of the inner circle.
View SolutionThe area of a circle whose radius is 6 cm, is trisected by two concentric circles. Find the radius of the smallest circle.
View SolutionThe area enclosed between the circumferences of two concentric circles is 16πcm2 and their radii are in the ratio 5 : 3. What is the area of the outer circle ?
View SolutionThe area enclosed by the circumference of two concentric circles is 423.5cm2. If the circumference of outer circle is 132 cm. Calculate the radius of the inner circle
View Solution
