Area of a segment
To find the area of a segment of a circle, we can follow these steps:
1. Understand the Components:
The area of a segment can be calculated using the area of the sector and the area of the triangle formed by the radius and the chord of the segment.
2. Formula for Area of Sector:
The area of the sector OAB can be calculated using the formula:
Area of Sector=θ360×πr2
where θ is the angle in degrees and r is the radius of the circle.
3. Determine the Height of the Triangle:
To find the area of triangle AOB, we need the height. If we drop a perpendicular from the center O to the chord AB, it bisects the chord and the angle θ. Thus, the height h can be expressed as:
h=rcos(θ2)
4. Determine the Base of the Triangle:
The base AB can be calculated as:
AB=2×rsin(θ2)
5. Calculate the Area of Triangle:
The area of triangle AOB can be calculated using the formula:
Area of Triangle=12×base×height
Substituting the values we found:
Area of Triangle=12×(2×rsin(θ2))×(rcos(θ2))=r2sin(θ2)cos(θ2)
Using the identity sin(x)cos(x)=12sin(2x):
Area of Triangle=12r2sin(θ)
6. Calculate the Area of the Segment:
Now, we can find the area of the segment APB by subtracting the area of the triangle from the area of the sector:
Area of Segment=Area of Sector−Area of Triangle
Substituting the formulas:
Area of Segment=(θ360×πr2)−(12r2sin(θ))
Final Formula:
Thus, the area of the segment APB is given by:
Area of Segment=θ360πr2−12r2sin(θ)
The area of a segment can be calculated using the area of the sector and the area of the triangle formed by the radius and the chord of the segment.
The area of the sector OAB can be calculated using the formula:
Area of Sector=θ360×πr2
where θ is the angle in degrees and r is the radius of the circle.
To find the area of triangle AOB, we need the height. If we drop a perpendicular from the center O to the chord AB, it bisects the chord and the angle θ. Thus, the height h can be expressed as:
h=rcos(θ2)
The base AB can be calculated as:
AB=2×rsin(θ2)
The area of triangle AOB can be calculated using the formula:
Area of Triangle=12×base×height
Substituting the values we found:
Area of Triangle=12×(2×rsin(θ2))×(rcos(θ2))=r2sin(θ2)cos(θ2)
Using the identity sin(x)cos(x)=12sin(2x):
Area of Triangle=12r2sin(θ)
Now, we can find the area of the segment APB by subtracting the area of the triangle from the area of the sector:
Area of Segment=Area of Sector−Area of Triangle
Substituting the formulas:
Area of Segment=(θ360×πr2)−(12r2sin(θ))
Thus, the area of the segment APB is given by:
Area of Segment=θ360πr2−12r2sin(θ)
Similar Questions
Consider the following statements :
1. Area of a segment of a circle is less than area of its corresponding sector.
2. Distance traveled by a circular wheel of diameter 2d cm in one revolution is greater than 6d cm.
Which of the above statements is/are correct ?
View SolutionIn the given figure, ∠AOB=30∘,O=12 cm Find the area of the segment. (π=3.14)

View Solution
Knowledge Check
Consider the following statements Area of segment of a circle is less than area of its corresponding sector. Distance travelled by a circular Wheel of diameter 2d cm in one revolution is greater than 6d cm. Which of the above statements is/are correct?
Aa. Only IBb. Only IICc. Both I and IIDd. neither I nor IIIn a circle of radius 14 cm, an arc subtends an angle of 120∘ at the centre. If √3=1.73 then the area of the segment of the circle is
A120.56cm2B124.63cm2C118.24cm2D130.57cm2
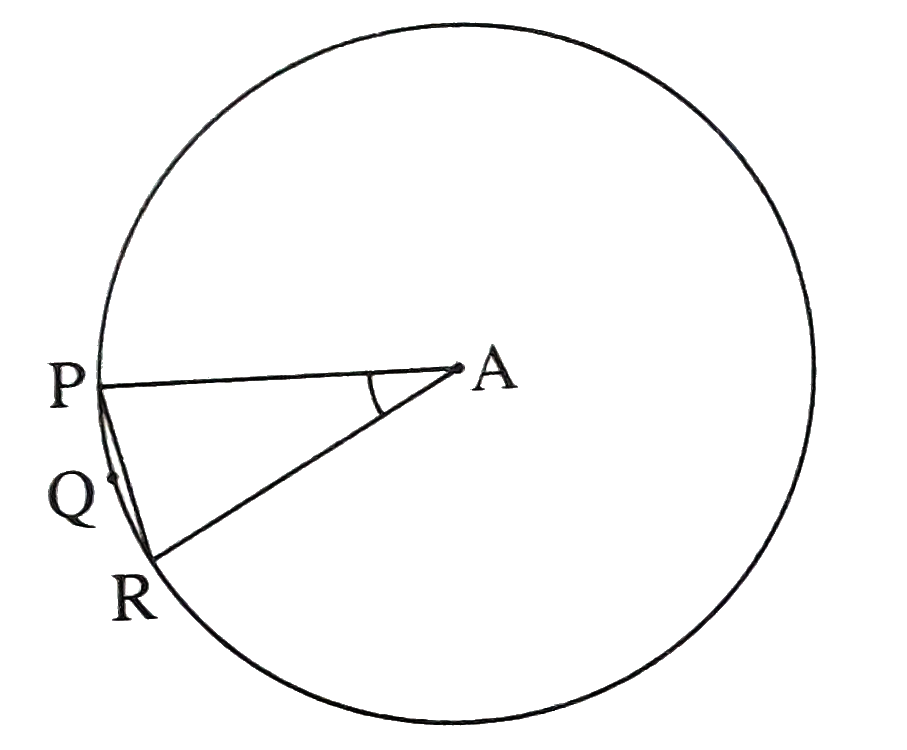
In the figure, if A is the centre of the circle. ∠PAR=30∘, AP=7.5,
find the area of the segment PQR. (π=3.14)
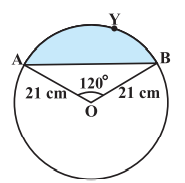
View SolutionFind the area of the segment AYB of circle, if radius of the circle centered at O is 21 cm and ∠AOB = 120o
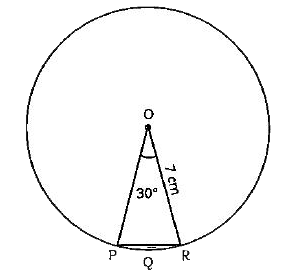
View SolutionWhat is the area of the segment PQR, in the given figure, if the radius of the circle is 7 cm?
(use π=227)
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find :
Area of the segment formed by the corresponding chord.
View SolutionFind the area of the segment shown in Figure, if radius of the circle is 21 cm and ∠AOB=120∘ ( Use π=227 )

View SolutionArea of the segment cut off from the parabola y2=4x by the line y=8x−1 is …...........
View Solution
