Examples :- If x,y∈{1;2;3;4} ;then which of the following are function in the given set ? (a)f1={(x;y):y=(x+1)}(b)f2={(x;y):x+y>4}(c)f3={(x,y):y
To determine which of the given sets are functions, we need to check each set against the properties of a function. A function from a set X to a set Y must satisfy two properties:
1. Every element in set X must be associated with at least one element in set Y.
2. No element in set X can be associated with more than one element in set Y.
Let's analyze each of the given sets step by step.
Given Sets:
1. f1 = {(x, y) : y = (x + 1)}
2. f2 = {(x, y) : x + y > 4}
3. f3 = {(x, y) : y = x^2} (assuming this is the intended definition based on the incomplete transcript)
Step 1: Analyze f1
- Definition: f1 = {(x, y) : y = (x + 1)}
- Set X = {1, 2, 3, 4}
- Calculating y for each x:
- For x = 1, y = 1 + 1 = 2 → (1, 2)
- For x = 2, y = 2 + 1 = 3 → (2, 3)
- For x = 3, y = 3 + 1 = 4 → (3, 4)
- For x = 4, y = 4 + 1 = 5 → (4, 5) (Note: 5 is not in set Y)
- Pairs formed: {(1, 2), (2, 3), (3, 4), (4, 5)}
- Check Properties:
- Property 1: Not all elements of X (1, 2, 3, 4) are mapped to Y since 5 is not in Y.
- Property 2: Each x maps to a unique y.
- Conclusion: f1 is not a function.
Step 2: Analyze f2
- Definition: f2 = {(x, y) : x + y > 4}
- Set X = {1, 2, 3, 4}
- Finding pairs:
- For x = 1: y can be 4 (1 + 4 > 4) → (1, 4)
- For x = 2: y can be 3 (2 + 3 > 4) → (2, 3)
- For x = 3: y can be 2 (3 + 2 > 4) → (3, 2)
- For x = 4: y can be 1 (4 + 1 > 4) → (4, 1)
- Pairs formed: {(1, 4), (2, 3), (3, 2), (4, 1)}
- Check Properties:
- Property 1: All elements of X are present.
- Property 2: Each x maps to a unique y.
- Conclusion: f2 is a function.
Step 3: Analyze f3
- Definition: f3 = {(x, y) : y = x^2}
- Set X = {1, 2, 3, 4}
- Calculating y for each x:
- For x = 1, y = 1^2 = 1 → (1, 1)
- For x = 2, y = 2^2 = 4 → (2, 4)
- For x = 3, y = 3^2 = 9 → (3, 9) (Note: 9 is not in set Y)
- For x = 4, y = 4^2 = 16 → (4, 16) (Note: 16 is not in set Y)
- Pairs formed: {(1, 1), (2, 4), (3, 9), (4, 16)}
- Check Properties:
- Property 1: Not all elements of X are mapped to Y since 9 and 16 are not in Y.
- Property 2: Each x maps to a unique y.
- Conclusion: f3 is not a function.
Final Conclusion:
- f1 is not a function.
- f2 is a function.
- f3 is not a function.
2. No element in set X can be associated with more than one element in set Y.
1. f1 = {(x, y) : y = (x + 1)}
2. f2 = {(x, y) : x + y > 4}
3. f3 = {(x, y) : y = x^2} (assuming this is the intended definition based on the incomplete transcript)
- Definition: f1 = {(x, y) : y = (x + 1)}
- Set X = {1, 2, 3, 4}
- Calculating y for each x:
- For x = 1, y = 1 + 1 = 2 → (1, 2)
- For x = 2, y = 2 + 1 = 3 → (2, 3)
- For x = 3, y = 3 + 1 = 4 → (3, 4)
- For x = 4, y = 4 + 1 = 5 → (4, 5) (Note: 5 is not in set Y)
- Pairs formed: {(1, 2), (2, 3), (3, 4), (4, 5)}
- Check Properties:
- Property 1: Not all elements of X (1, 2, 3, 4) are mapped to Y since 5 is not in Y.
- Property 2: Each x maps to a unique y.
- Conclusion: f1 is not a function.
- Definition: f2 = {(x, y) : x + y > 4}
- Set X = {1, 2, 3, 4}
- Finding pairs:
- For x = 1: y can be 4 (1 + 4 > 4) → (1, 4)
- For x = 2: y can be 3 (2 + 3 > 4) → (2, 3)
- For x = 3: y can be 2 (3 + 2 > 4) → (3, 2)
- For x = 4: y can be 1 (4 + 1 > 4) → (4, 1)
- Pairs formed: {(1, 4), (2, 3), (3, 2), (4, 1)}
- Check Properties:
- Property 1: All elements of X are present.
- Property 2: Each x maps to a unique y.
- Conclusion: f2 is a function.
- Definition: f3 = {(x, y) : y = x^2}
- Set X = {1, 2, 3, 4}
- Calculating y for each x:
- For x = 1, y = 1^2 = 1 → (1, 1)
- For x = 2, y = 2^2 = 4 → (2, 4)
- For x = 3, y = 3^2 = 9 → (3, 9) (Note: 9 is not in set Y)
- For x = 4, y = 4^2 = 16 → (4, 16) (Note: 16 is not in set Y)
- Pairs formed: {(1, 1), (2, 4), (3, 9), (4, 16)}
- Check Properties:
- Property 1: Not all elements of X are mapped to Y since 9 and 16 are not in Y.
- Property 2: Each x maps to a unique y.
- Conclusion: f3 is not a function.
- f1 is not a function.
- f2 is a function.
- f3 is not a function.
Similar Questions
Given the graph of f(x), draw the graph each one of the following functions :
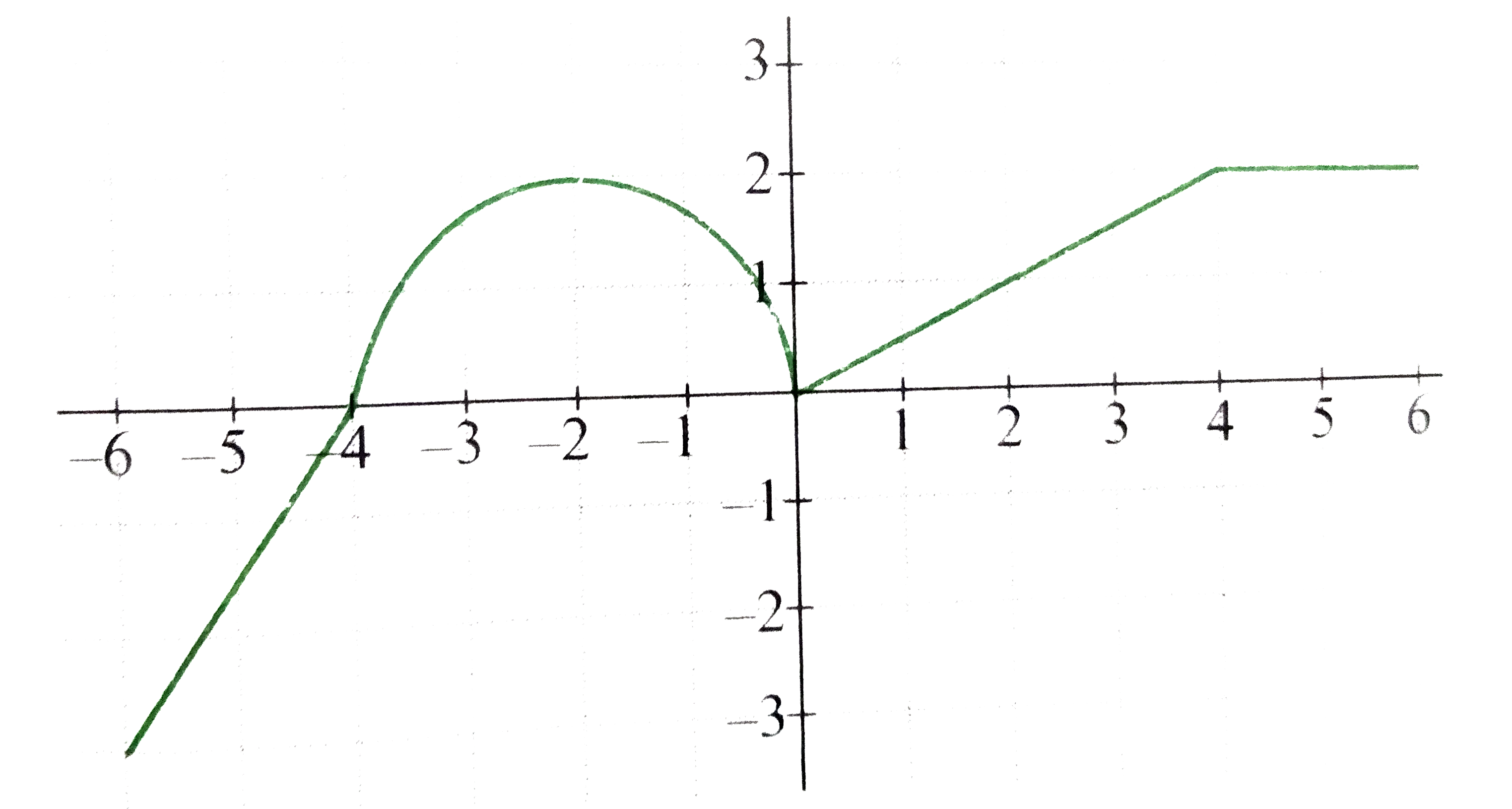
(a) y=f(x)+3 (b) y=−f(x)+2
(c ) y=f(x+1)−2 (d) y=−f(x−1)
(e ) y=f(−x) (f) y=f(|x|)
(g) y=f(1−x)
View SolutionGiven the graph of y=f(x).

Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View Solution
Knowledge Check
Which of the following functions satisfies the condition
f(x+yx−y)=f(x)+f(y)f(x)−f(y)?Af(x)=xBf(x)=ax+bCf(x)=2xDf(x)=x2Let f(x) be a real valued function such that f(0)=12 and f(x+y)=f(x)f(a-y)+f(y)f(a-x),∀x,y∈R, then for some real a,
Af(x) is a periodic functionBf(x) is a constant functionCf(x)=12Df(x)=cosx2
Let f(x) be a function such that f(x).f(y)=f(x+y), f(0)=1,f(1)=4. If 2g(x)=f(x).(1−g(x))
View SolutionIf f(x,y)=2x2−5xy+3y2 , find the following:
f(1,−1)
View SolutionIf a function satisfies (x−y)f(x+y)−(x+y)f(x−y)=2(x2y−y3)∀x,y∈Randf(1)=2, then
View SolutionIf the function f(x) satisfies the relation f(x+y)=y|x−1|(x−1)f(x)+f(y) with f(1)=2. then limx→1f'(x) is
View SolutionIf 2x+3|y|=4y, then y as a function of x i.e. y=f(x), is -
View SolutionIf f:R→R be a function such that f(x+2y)=f(x)+f(2y)+4xy,∀x,y and f(2)=4 then, f(1)−f(0) is equal to
View Solution
