A particle is dropped from the top of a tower.
(a) Find the ratio of displacement in successive time interval t0.
(b) Find the ratio of time in falling successive distances h.
Video Solution
Text Solution
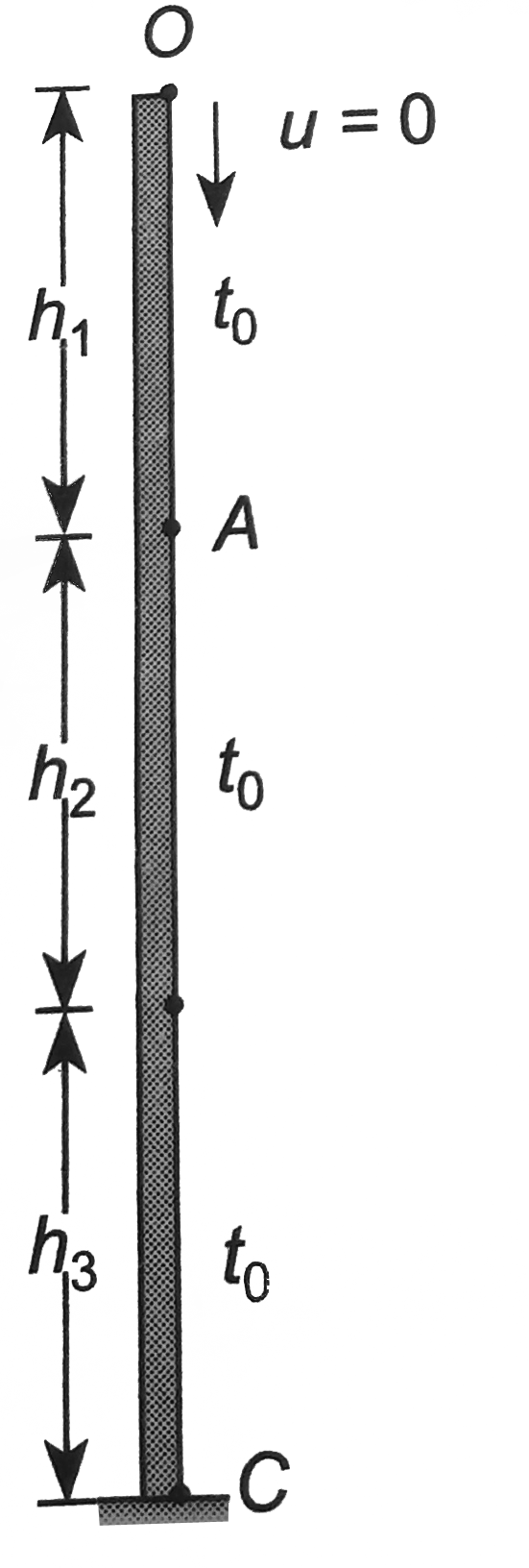
O to A: h1=12gt20…(i)
O to B: h1+h2=12g(t0+t0)2=4.12gt20
h2=(4−1)12gt20
=3.12gt20…(ii)
O to C: h1+h2+h3=12g(t0+t0+t0)2
=9.12gt20
h3=(9−4)12gt20
=5.12gt20...(iii)
h1:h2:h3:...=12gt20:3.12gt0:5.12gt20:...
=1:3:5:...
Recall: If a particle is moving in a straight line under constant acceleration//deceleration, the ratio of displacement in successive time-intervals are in the ratio of add numbers.
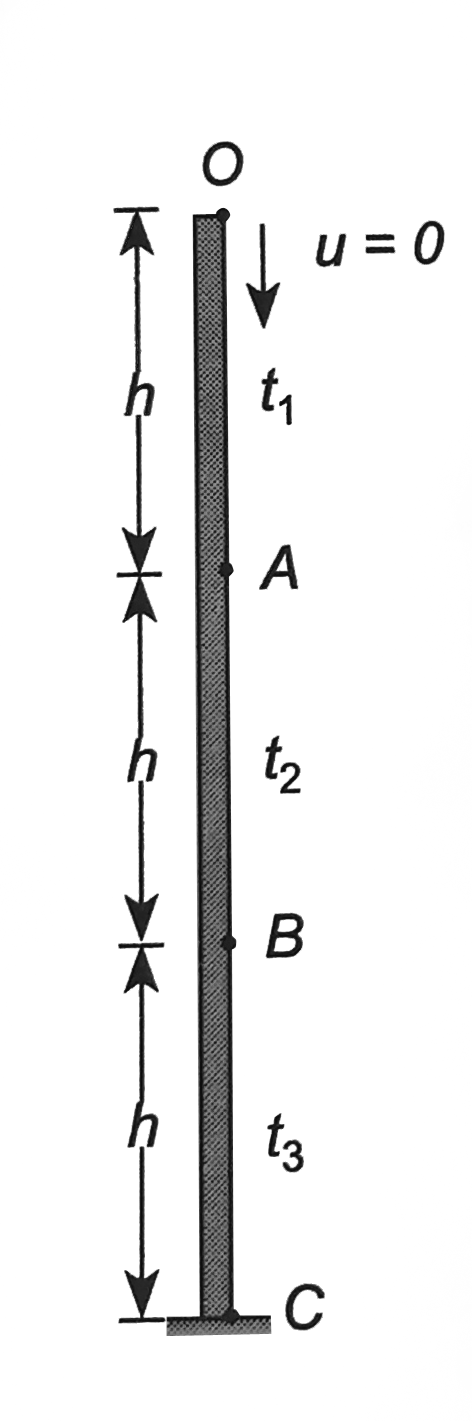
(b) O to A: h=12gt21
t1=√2hg...(i)
O to B: h+h=12g(t1+t2)2
t1+t2=√4hg
t2=√4hg−√2hg...(ii)
O to C: h+h+h=12g(t1+t2+t3)2
t1+t2+t3=√6hg
t3=√6hg−√4hg...(iii)
t1:t2:t3∴...=√2hg:(√4hg−√2hg):(√6hg−√4hg)...
=1:(√2−1):(√3−√2)...
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The ration of the distance traversed, in successive intervals of time by a body, falling from rest, are
A1 : 3 : 5 : 7 : 9 : …B2 : 4 : 6 : 8 : 10 : …C1 : 4 : 7 : 10 : 13 : …DNone of the aboveA particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal height h is.
At1:t2:t3=3:2:1Bt1:t2:t3=1:(√2−1):(√3−2)Ct1:t2:t3=1:√2:√3Dt1:t2:t3=1:(√2−1):(√3−√2)A body falls from a large height. The ratio of distance traveled in each time interval t0 during t=0 to t=3t0 of the journey is
A1:4:9B1:2:4C1:3:5D1:2:3
A particle is dropped the top of a tower. Its displacement in the first three seconds and in the last second is the same. Find the height of the tower.
View SolutionA particle is dropped from the top of a tower. If it falls half of the height of the tower in its last second of journey, find the time of journey.
View SolutionA particle is dropped from the top of a tower. Its covered distance in last 1 sec is equal to distance covered by particle in 1st3s. Find height of tower.
View SolutionA particle is dropped from the top of a tower. During its motion it covers 925 part of height of tower in the last 1 second Then find the height of tower.
View SolutionA particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View Solution
