A ball is thrown vertically up with a velocity u. It passes three points A,B and C in its upward journey with velocities us,u3 and u4, respectively. Find ABBC.
To solve the problem, we need to find the ratio of the distances AB and BC that a ball travels when thrown vertically upwards with an initial velocity u and passing through points A, B, and C with given velocities.
1. Identify the velocities at points A, B, and C:
- Velocity at point A, vA=u2
- Velocity at point B, vB=u3
- Velocity at point C, vC=u4
2. Use the kinematic equation:
We will use the equation v2=u2+2as where:
- v is the final velocity,
- u is the initial velocity,
- a is the acceleration (which is −g for upward motion),
- s is the displacement.
3. Calculate displacement AB:
- For the segment AB:
v2B=v2A+2(−g)(AB)
Substituting the values:
(u3)2=(u2)2−2g(AB)
u29=u24−2g(AB)
Rearranging gives:
2g(AB)=u24−u29
Finding a common denominator (36):
2g(AB)=9u236−4u236=5u236
Thus,
AB=5u272g
4. Calculate displacement BC:
- For the segment BC:
v2C=v2B+2(−g)(BC)
Substituting the values:
(u4)2=(u3)2−2g(BC)
u216=u29−2g(BC)
Rearranging gives:
2g(BC)=u29−u216
Finding a common denominator (144):
2g(BC)=16u2144−9u2144=7u2144
Thus,
BC=7u2288g
5. Calculate the ratio ABBC:
ABBC=5u272g7u2288g=5u2⋅288g72g⋅7u2
The u2 and g cancel out:
ABBC=5⋅28872⋅7=1440504=207
Final Answer:
ABBC=207
- Velocity at point A, vA=u2
- Velocity at point B, vB=u3
- Velocity at point C, vC=u4
We will use the equation v2=u2+2as where:
- v is the final velocity,
- u is the initial velocity,
- a is the acceleration (which is −g for upward motion),
- s is the displacement.
- For the segment AB:
v2B=v2A+2(−g)(AB)
Substituting the values:
(u3)2=(u2)2−2g(AB)
u29=u24−2g(AB)
Rearranging gives:
2g(AB)=u24−u29
Finding a common denominator (36):
2g(AB)=9u236−4u236=5u236
Thus,
AB=5u272g
- For the segment BC:
v2C=v2B+2(−g)(BC)
Substituting the values:
(u4)2=(u3)2−2g(BC)
u216=u29−2g(BC)
Rearranging gives:
2g(BC)=u29−u216
Finding a common denominator (144):
2g(BC)=16u2144−9u2144=7u2144
Thus,
BC=7u2288g
ABBC=5u272g7u2288g=5u2⋅288g72g⋅7u2
The u2 and g cancel out:
ABBC=5⋅28872⋅7=1440504=207
ABBC=207
Topper's Solved these Questions
Similar Questions
A particle is thrown vertically upward with a velocity of u. Find its time of flight.
View SolutionRead the given passage and answer the following questions.
A body is thrown vertically up with a velocity u as shown in the figure. It passes through points P and Q in its upward journey and reaches the maximum height at point R. Here PQPR=716,OP=2u245 , and take g=10m/s2
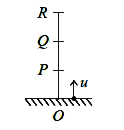
Find the velocity of the particle at point P.
View Solution
Knowledge Check
A player throws a ball vertically upwards with velocity u. At highest point,
Aboth the velocity and acceleration of the ball are zero.Bthe velocity of the ball is u but its accelerationCthe velocity of the ball is zero but its acceleration is g.Dthe velocity of the ball is u but its acceleration is g.A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is
Au/gBu2/2gCu2/gDu/2gA body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,
Au/gBu2/2gCu2/gDu/2g
Read the given passage and answer the following questions.
A body is thrown vertically up with a velocity u as shown in the figure. It passes through points P and Q in its upward journey and reaches the maximum height at point R. Here PQPR=716,OP=2u245 , and take g=10m/s2
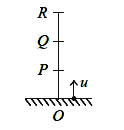
Find the time taken by the particle to reach highest point R.
View SolutionAn object is thrown upward with a velocity u, then displacement -time graph is
View SolutionA body is thrown vertically upwards with a velocity u . Find the true statement from the following
View SolutionA ball is thrown vertically upward with a velocity u from the top of a tower. If it strikes the ground with velocity 3u, the time taken by the ball to reach the ground is
View SolutionA body is thrown vertically upward with velocity u. The distance traveled by it in the fifth and the sixth second are equal. The velocity u is given by
View Solution