A particle is moving in sand under acceleration a=g−λy2, where lambda is a positive constant and y is the distance traveled on the y-axis. If the initial velocity is v0 and after traveling a distance ym, the particle stops, find λ (the motion is along the y-axis).
a=g−λy2
vdvdy=g−λy2
∫0v0vdv=∫ym0(g−λy2)dy
∣∣∣v22∣∣∣0v0=∣∣∣gy−λy33∣∣∣ym0
0−v202=gym−λy3m3
λy3m3=gym+v202=2gym+v202
λ=6gym+3v202y3m
Topper's Solved these Questions
Similar Questions
A particle moves uniformly with speed v along a parabolic path y=kx2, where k is a positive constant. Find the acceleration of the particle at the point x = 0.
View SolutionA particle starts moving from position of rest under a constant acceleration if it travels a distance x in t second, what distance will it travel in next t second?
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts moving from rest under uniform acceleration it travels a distance x in the first two seconds and a distance y in the next two seconds. If y=nx, then n=
A1B2C3D4 - Question 2 - Select One
A particle starts moving from rest under a constant acceleration. It travels a distance x in the first 10 sec and distance y in the next 10 sec, then
Ay = xBy = 2xCy = 3xDy = 4x - Question 3 - Select One
A particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
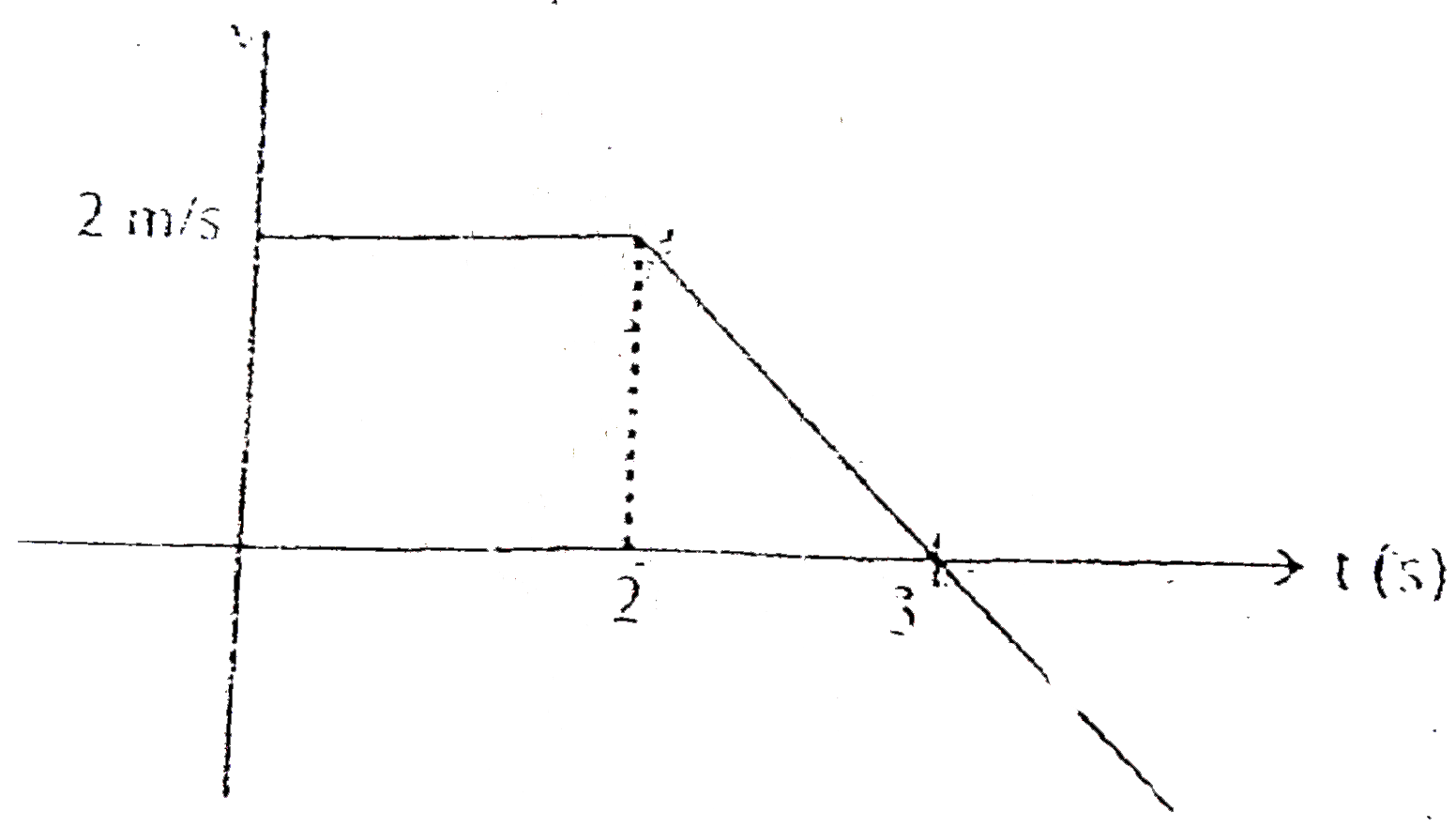 A1mB9mC3mD7m
A1mB9mC3mD7m
A particle having a velocity v=v0 at t=0 is accelerated at a rate |a|=α√v, where α is a positive constant. Calculate the distance travelled before the particle is brought to rest.
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View SolutionA particle of charge q and mass m moves rectilinearly under the action of an electric field E=A−Bx, where B is a positive constant and x is a distance from the point where the particle was initially at rest. The distance travelled by the particle till it comes to rest is αAβB. Find (α+β).
View SolutionA particle is moving under a constant acceleration of 3m/s2. The initial velocity of the particle is 10m/s. calculate the distance travelled by the particle is 5s and also in th 5th second of its motion.
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :View Solution

