A particle is moving in a straight line under acceleration a=54−18t. The particle starts from the origin.
(a) Sketch the a-t, v-t and s-t graph.
(b) Find the distance traveled in the first 9 s. (Acceleration is in m/s2, time is in second)
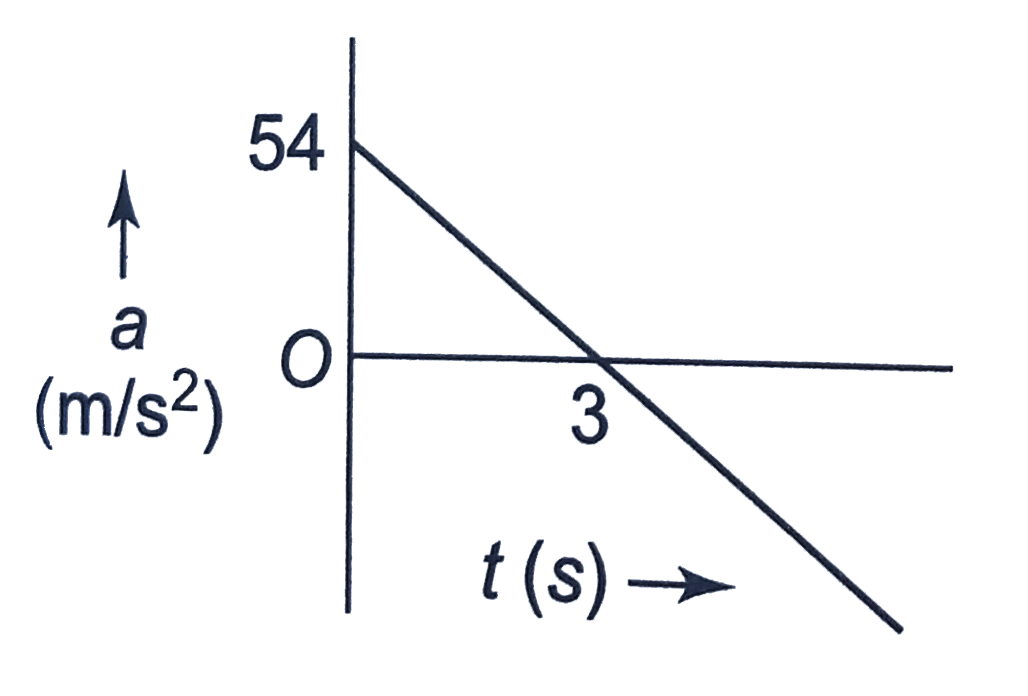
(a) (i) a=54−18t
t=0,a=54m/s2
a=0⇒54−18t=0⇒t=3s
t<3s,a=+ve
t>3s,a=−ve
Shape: y=54−18x(straight line)
(ii) a=54−18t
dvdt=54−18t
∫v0dv=∫t0(54−18t)dt
|v|v0=∣∣∣54t−18t22∣∣∣t0
v=54t−9t2
t=0,v=0
v=0⇒54t−9t2=0
9t(6−t)=0⇒t=0,t=6s
v is maximum if dvdt=a=54−18t=0
For t=3s
v=vmax=54×3−9×32=162−81=81m/s
For t gt 6 s, v=-ve
Shape: y=54x−9x2 (parabola, open downward)
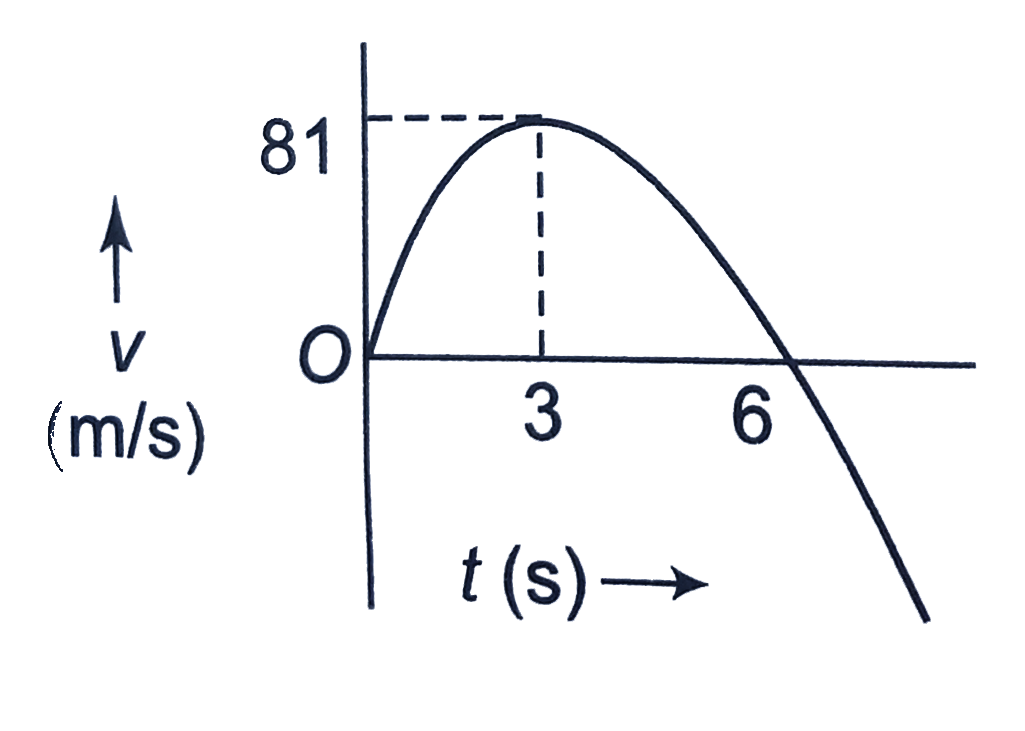
(iii) s-t graph
v=54t−9t2
dsdt=54t−9t2
∫s0ds=∫t0(54t−9t2)dt
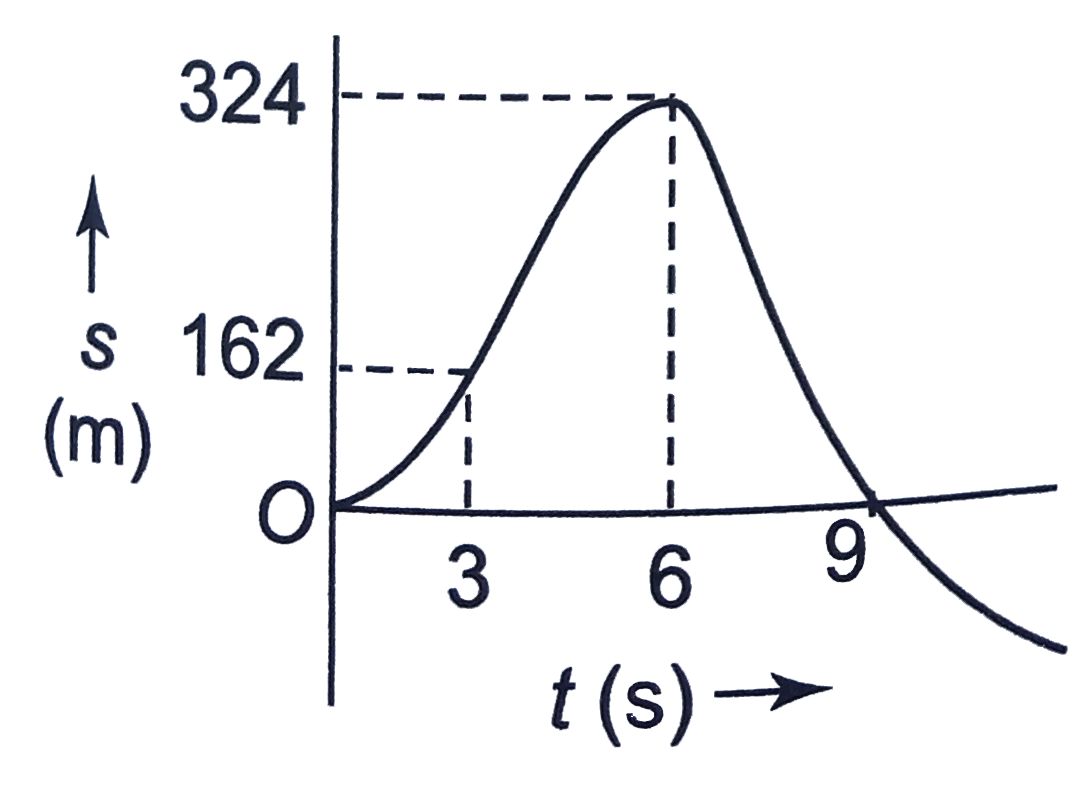
s=27t2−3t3
t=0,s=0
s=0⇒27t2−3t3=0⇒3t(9−t)=0
⇒t=0,t=9s
s is maximum if dsdt(=v)=0
⇒t=6s
smax=27(6)2−3(6)3=324m
For t gt 9 s, s=−ve
For t=0 to t=3s, velocity is increasing, i.e. slope of s-t graph is increasing.
For t=3 to 6s, velocity is decreasing and v gt 0, a lt 0, the particle is slowing down, slope of the s-t graph is decreasing.
For t gt 6 s, v lt 0, a 0 lt 0, the particle is speeding up.
For t=3s,s=162m
For t=6s,s=324m
For t=9s,s=0
(b) Distance in 9 s
Velocity changes sign at t=6s
Distance=∫60vdt+∣∣∣∫96vdt∣∣∣
=324+|−320|=648m
Topper's Solved these Questions
Similar Questions
A partical is moving in a straight line under constant acceleration 4m/s2. The motion starts from rest. Sketch v-t and s-t graph for the duration t=0 to t=5s.
View SolutionA particle is moving in a straight line under constant acceleration alpha. If the intial velocity is v0, sketch the v-t and s-t graphs. (v0>0).
View Solution
Knowledge Check
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
A15 mB30 mC45 mD60 mThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
Av0t+16bt3Bv0t+13bt3Cv0t+13bt2Dv0t+12bt2
A particle moves along a straight line.The acceleration of the particle as function of time is given by a=6t−12 .Initial velocity of particle is 9ms .Find distance (in meters) travelled by particle in 4 seconds.
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q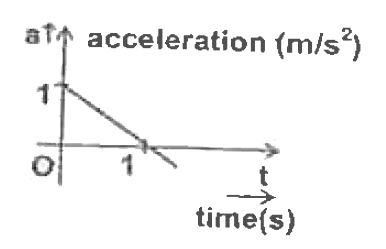
View Solution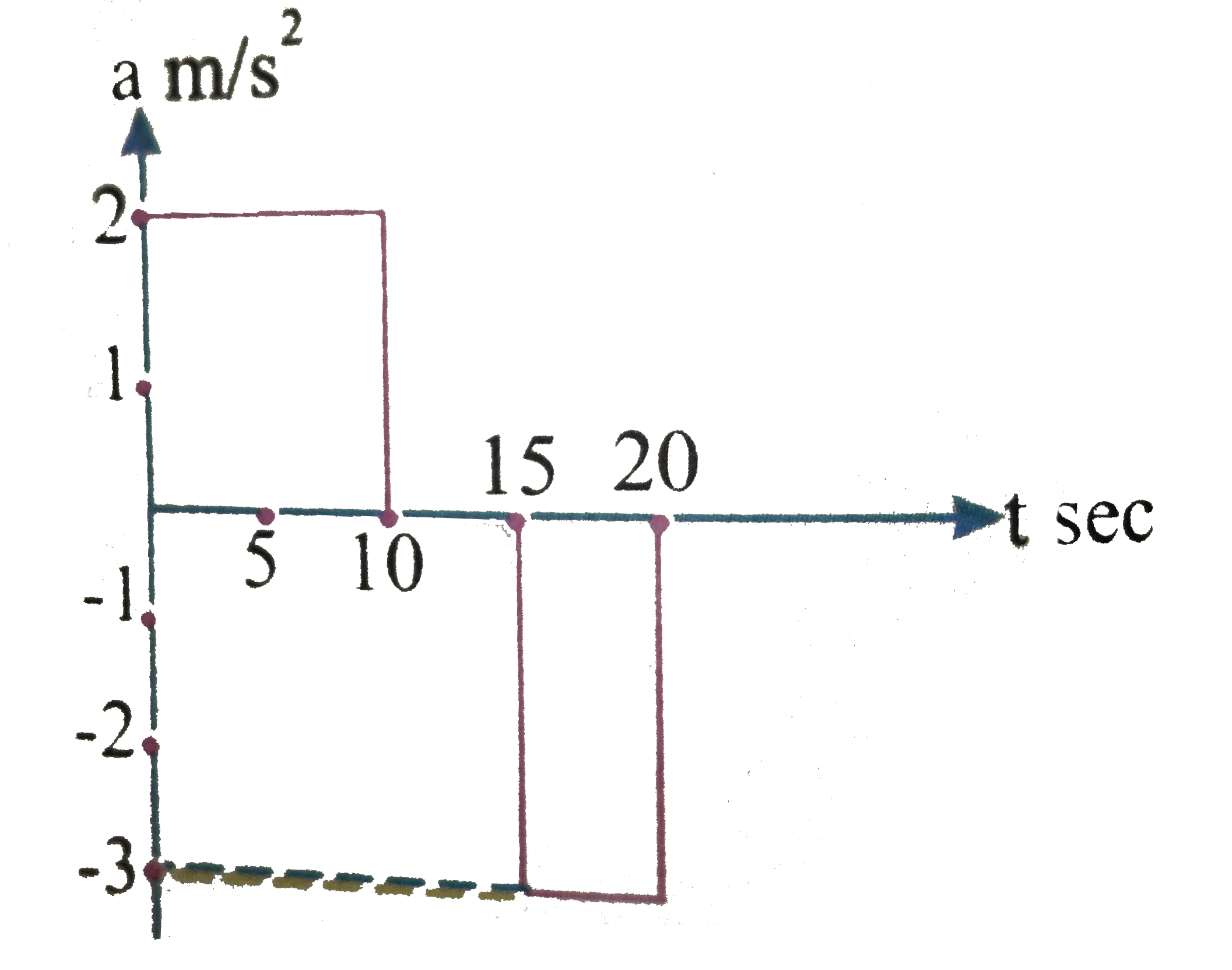
A particle starts from rest and accelerated as shown in the graph. Determine
(a). The particle's speed at t=10s and at t=20s
(b). The distance travelled in the first 20s.
View SolutionA particle is moving with an acceleration given by, a=−cost ; where time t is in seconds and a is in ms2 . It is given that at t=0, u=0 and x=1 .Find distance travelled by particle from π to 2π.
View SolutionA particle is moving in a straight line and its acceleration-time graph is shown below. At t=0, the particle is at rest. Find the velocity of the particle at t=3s,6s and 8s. Also sketch the v-s graph.
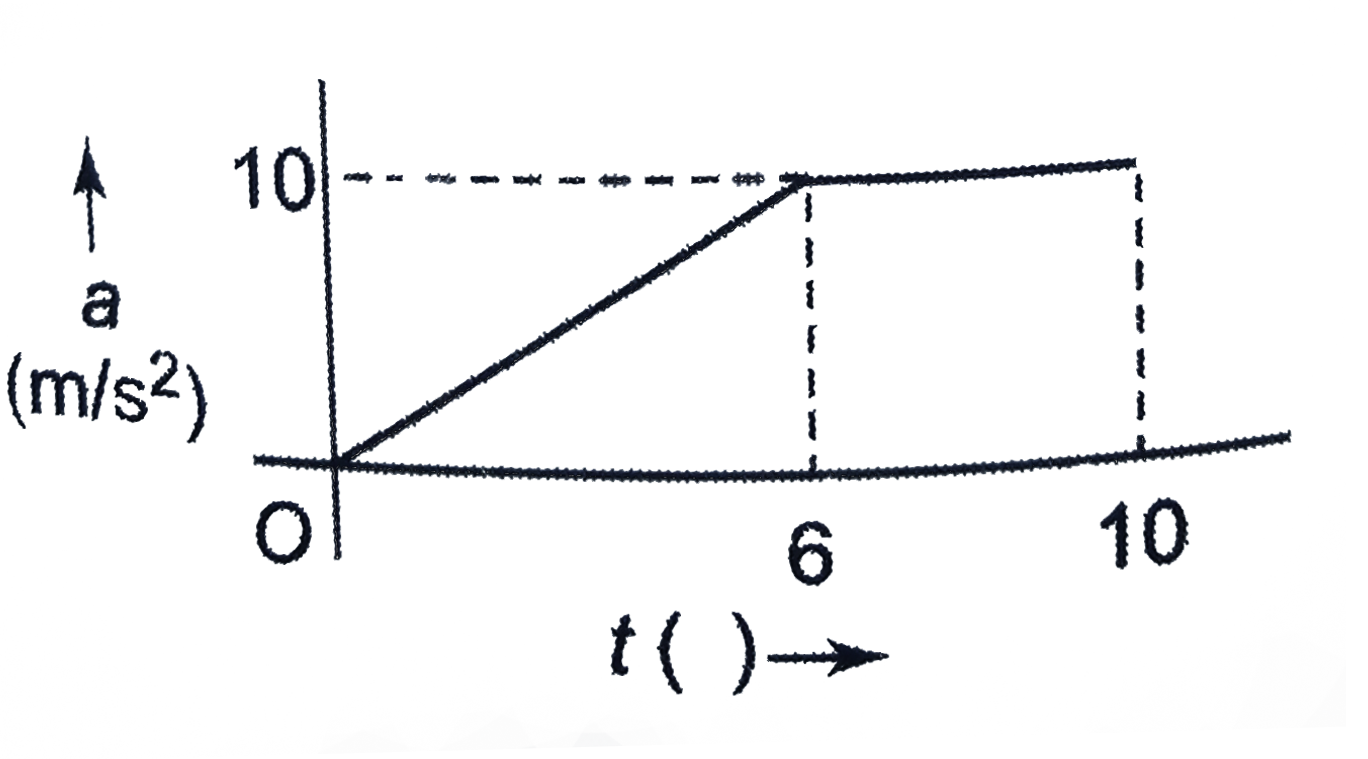
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View Solution