Question

Calculate Area Of A Triangle ?

Explanation

Area of Triangle

In this lesson, you will learn about the area of the triangle. We will also look at some solved examples to clear your confusions, also for better understanding of the concept. The total space, which is enclosed by a particular triangle, is called the area of a triangle.

For a given triangle, the basic formula is A = ½ x b x h. Here ‘b’ is the base where ‘h’ is the height of the given triangle. It does not matter whether it is an isosceles, scalene, or equilateral.

Example, if you need to find the area of a triangle that has got a base of 5 cm and height of 4 cm, then we can use the formula as under:

Area of a triangle = ½ x b x h

                           = ½ x 5 cm x 4 cm

                           = ½ x 20 cm²

                           = 10 cm²   

When we say the area in general, it refers to the region that is occupied inside the boundary of a figure or a flat object. Here, when it comes to its measurement, it is done in square units with the standard unit being square meters (m².) There are also pre-defined formulas for rectangles, squares, triangles, squares, etc. for the computation of area.

Area of Triangle Formulae

We will proceed further to discuss the area of the triangle formulae for the different types of triangles where we will also have some look at the examples as well.

Area of Triangle

Area = ½ x base x perpendicular height

Here is the formula for the area of a triangle:

Area of a Triangle = ½ (b x h) square units ( b = base  and  h = height )

We will try to calculate the area of a triangle by using a given figure with the formula at the end. We will now move on to understand the area formulas for the different types of triangles.  Here, you can get the right understanding of the area of a right-angled triangle, an equilateral triangle, and an isosceles triangle. You would also be able to use Heron’s formula to find the area of a triangle.

Area of a Right-Angled Triangle

Area of a Right Triangle (A) = ½ × Base × Perpendicular

A right-angled triangle has one angle at 90⁰ and the other two acute angle sums to 90⁰. It is also known as a right triangle. The length of the perpendicular side is the height of the triangles.

Area of an Equilateral Triangle

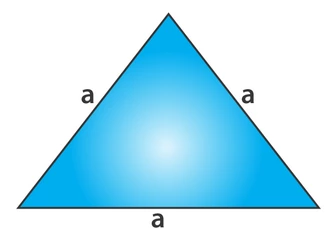
Area of an Equilateral Triangle (A) = (√3)/4 × (side)²

The sides of an equilateral triangle are equal. The vertex of the triangle where the perpendicular is drawn to the base divides the base into two equal parts. It is required to know the measurement of its sides in order to find out the area of the equilateral triangle.

Area of an Isosceles Triangle

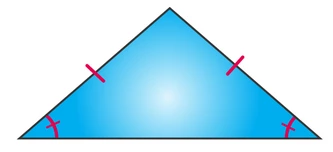
Area of an Isosceles Triangle = A = ½ (base × height)

When it comes to an isosceles triangle, the two sides are equal, and also the angle opposite the equal sides is also equal.

Perimeter of a Triangle

Now, let us come to the perimeter of a Triangle. Well, the distance which is covered around the triangle is called as the perimeter of a triangle. It is calculated by taking the sum of all the three sides.

The formula for the perimeter of a triangle (P) = a + b + c units  ( a, b and c are the sides of the triangle.)

Related Videos:

• Area and Perimeter of rectangle, square and triangles


• Calculate the area of an equilateral triangle


• Area and Perimeter of all type of parallelogram and rhombus


• Pythagoras Theorem

 

Area of Triangle with 3 Sides using Heron’s Formula

Heron’s formula is used to find the area of the triangle with 3 sides. There are two steps that are used in Heron’s formula. Coming to the first step in finding the semi perimeter of a triangle, it is done by taking the measurement of three sides of a given triangle. On the other hand, the next step is the application of the measures of the sides of a triangle such as a, b and c along with the semi-perimeter of triangle value so as to calculate the area of a triangle.

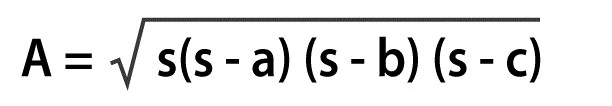
Here ‘s’ is semi-perimeter of the triangle = (a + b + c) / 2

We have seen that the area of different triangles could be obtained by making use of the triangle formula as per the dimensions provided.  But you need to know that it is not simple to calculate the height for a given side of a triangle. So, we make use of Heron’s formula while calculating the area of the triangle that has unequal lengths.

We hope that you now have a clear idea about the area of a triangle, area of triangle formula, etc. In order to make it more convenient to understand these concepts, we have provided you with some solved examples.

Area of Triangles Examples

Example 1:

An acute triangle has a base of 15 inches and a height of 6 inches. Calculate its area?

Solution:

A = (½) × b × h sq.units

⇒ A = (½) × (15 in) × ( 6 in)

⇒ A = (½) × (90 in²)

⇒ A = 45 in²

Example 2:

A right-angled triangle has a base of 8 cm and a height of 10 cm. Find the area of the triangle.

Solution:

Area of triangle = (½) × b × h sq.units

⇒ A = (½) × ( 8 cm) × ( 10 cm)

⇒ A = (½) × (80cm²)

⇒ A = 40 cm²

Example 3:

An obtuse-angled triangle has a base of 6 cm and a height 8 cm. Find the area of the triangle.

Solution:

Area of triangle = (½) × b × h sq.units

⇒ A = (½) × (6 cm) × ( 8 cm)

⇒ A = (½) × (48 cm²)

⇒ A = 24 cm²

Example 4:

An acute triangle has a base of 18 inches and a height of 8 inches. Calculate its area?

Solution:

Area of triangle = (½) × b × h sq.units

⇒ A = (½) × (18 in) × ( 8 in)

⇒ A = (½) × (124 in²)

⇒ A = 62 in²

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 9 Chapter Coordinate Geometry


• NCERT Solution for Maths Class 10 Chapter Coordinate Geometry