Determine electric field at point P or O in the following cases , take 14π∈0.Qd2=E0.
(a) 
(b) 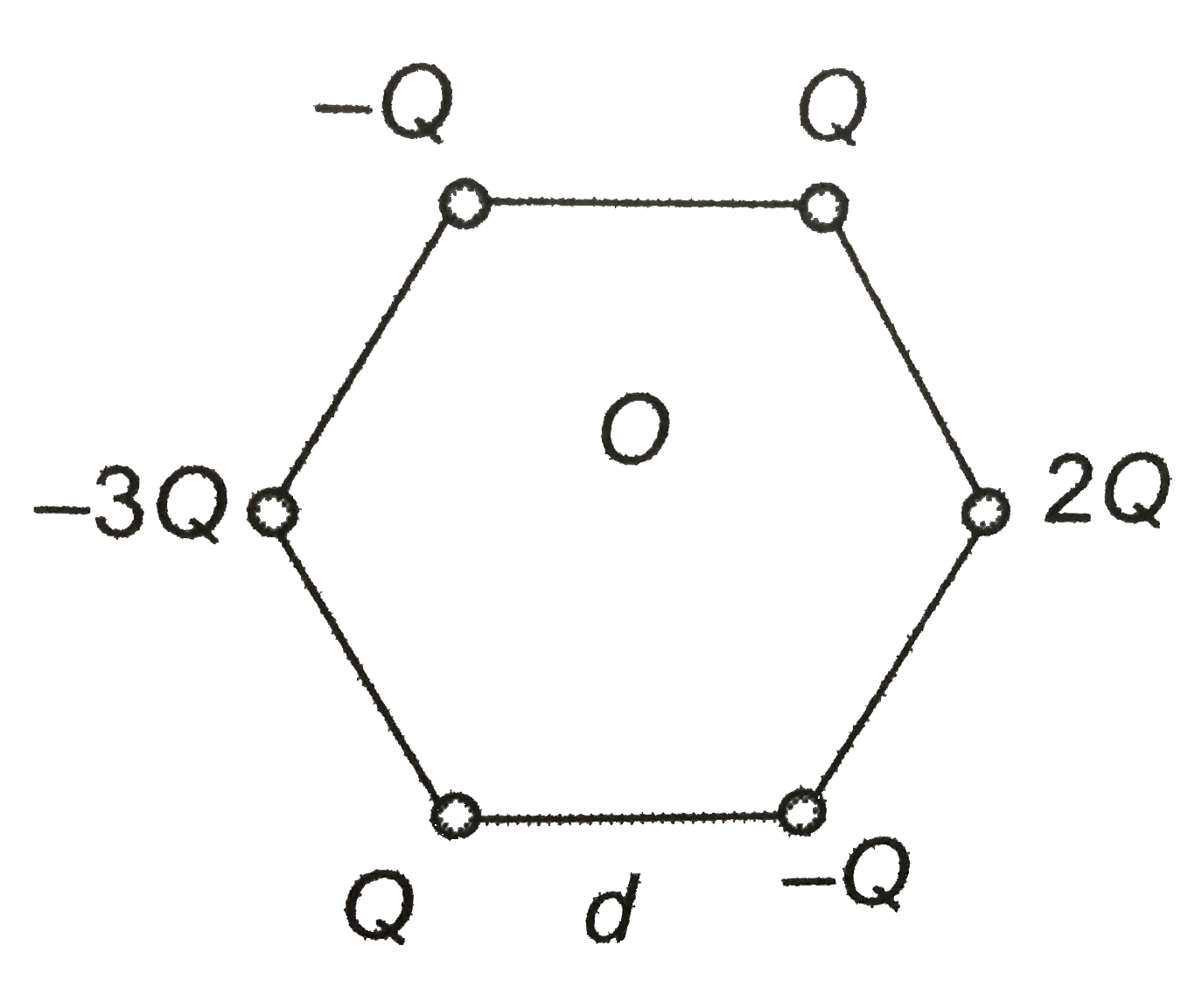
(a) Electric field at P :
Due to 9Q,E1=14π∈0.9Q(3d)2=14π∈0Qd2=E0, towards right
Due to 4Q,E2=14π∈0.4Q(2d)2=E0, towards right
Due to −Q,E3=14π∈0.Qd2=E0 , towards left
Resultant field at P:
Ep=E1+E2−E3=E0 , towards right
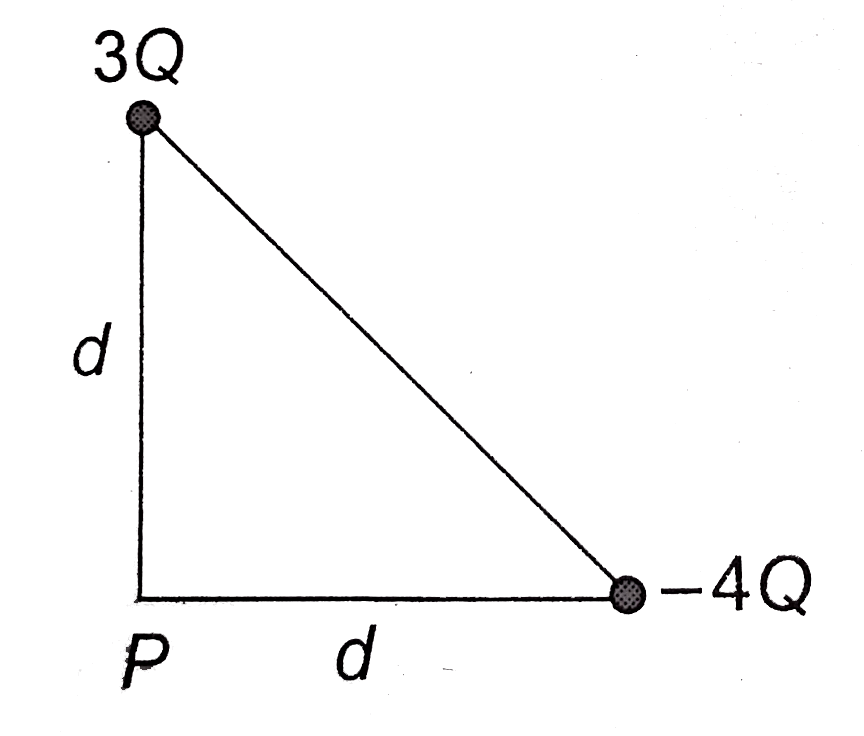
(b) Electric field at P :
Due to 3Q,E1=14π∈0.3Qd2=3E0, downward
Due to −4Q,E2=14π∈0.4Qd2=4E0, towards right
Ep=√E21+E22=5E0
tanα=3E04E0=34⇒α=tan−1(3/4)
(c ) Electric field at P:
QatA,E1=14π∈0.Qd2=E0 , along AP
QatB,E2=E0 , along BP
Ep=E0cos30∘×2=√3E0
(d) At P:
4Q,E1=14π∈0.4Q(2d)2=E0 , along BP
−2Q at left top , E2=14π∈0.2Q(√2d)2=E0 , along PA
−2Q at right bottom , E3=14π∈0.2Q(√2d)2=E0 , along PC
The resultant of E2 and E3 is √2E0 at angle 45∘ with either
E2orE3. Net electric field at P,(√2−1)E0 , at angle 45∘
(e) Electric field at O:
9Q at A,E1=14π∈0.9Q(5d)2=9E025 , along AO
−9Q at B , E2=9E025, along OB
−16Q at C,E3=14π∈0.16Q(5d)2=16E025 , along OC
16QatD,E4=16E025 , along DO
cosα=8d10d=45
Ep=E0cosα×2=E0×45×2=8E05
Alternatively :
The direction of electric fields due to 16Q and −9Q is same and these charges are placed at same separation from O , so we can combine these charges as (16Q+9Q) or (−9Q−16Q).
(f) The electric fields at O by pairs (Q,Q),(−Q,−Q) is zero
E0=14π∈0.5Qd2=5E0 , towards left











Topper's Solved these Questions
Similar Questions
Find the net electric force on charge q in the following cases , take 14π∈0Qqd2=F0.
(a)
(e) The point charges Q,80Q,27Q,...,1000Q are placed at x=d,2d,3d,....,10d. A point charge q is placed at origin.
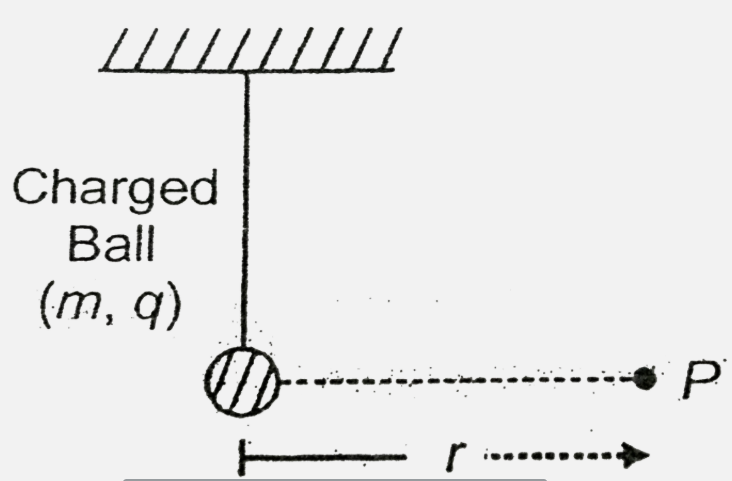
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View Solution
Knowledge Check
What are the units of K14π∈0 ?
AC2N−1m−2BC−2N−1m2CC2N1m2DunitlessIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: If E be electric field at a point , in free space then energy density at that point will be 12ε0E2 .
R , electrostatic field is a conservative field .AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion , then mark (1).BIf both Assertion & Reason are true but the reason is not correct explanation of the assertion then mark (2)CIf Assertion is true statement but Reason is false, then mark (3)DIf both Assertion and Reason are false statements , then mark (4).
The electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .

View SolutionWhat are the units of K14π∈0 ?
View SolutionAn infinite number of charges each equal to q are placed along the x-axis at x=1m,x=2m,x=4m,x=8m, ... and so on. Find the potential and electric field at the point x = 0 due to this set of charges. What will be potential and electric field ifin the above set up if the consecutive charge have opposite sign?
[q2π∈0,q3π∈0,q6π∈0,q5π∈0]
View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: If E be electric field at a point , in free space then energy density at that point will be 12ε0E2 .
R , electrostatic field is a conservative field .
View SolutionFind the magnitude of the electric field at the point P in the configuration shown in figure- 1.219 (a), (b) and (c ) for d>>a take 2qa=P.
[(a)q4π∈0d2,(b)2q2π∈0d3,(c)q4π∈0d2√1+4a2d2]

View SolutionDetermine whether the following points are collinear
D(−2,−3),E(1,0),F(2,1)
View Solution
