Question

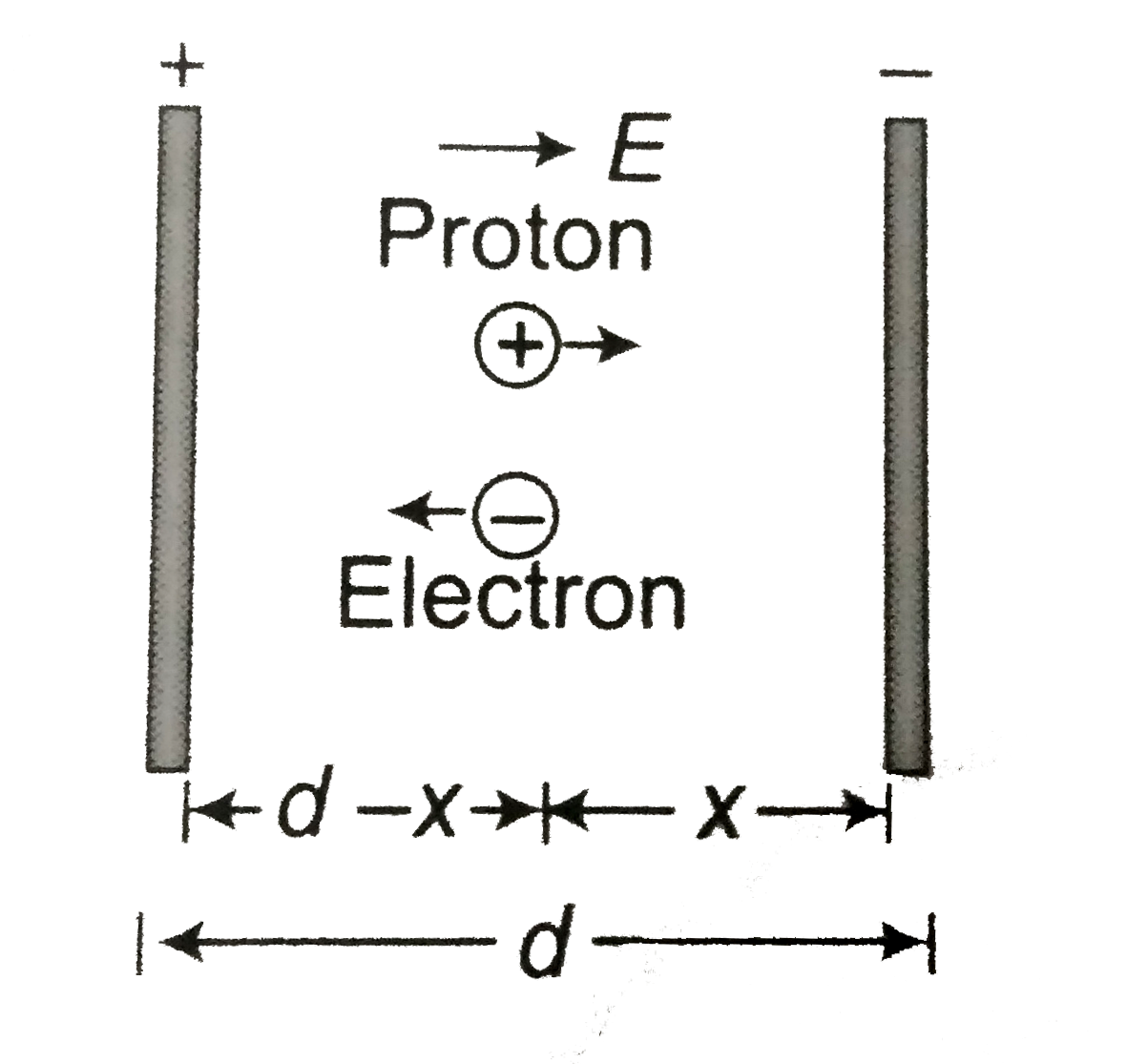
The distance between charged parallel plates is $d$. An electron -proton is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as electron reaches the positive plate. At consider only electric force. The mass of electron is $m_e$ and mass of proton is $m_p$.The electric field between plates is $E$.

Explanation

Let the pair be released at distance `x` from the negative plate.
Photon : `a_(p) = (eE)/(m_(p))`
`s = ut + (1)/(2) at^(2)`
`x = 0 + (1)/(2) (eE)/(m_(p)) t^(2)` ….(i)
Electron : `a_(e ) = (eE)/(m_(e))`
`d -x = 0 + (1)/(2) (e E)/(m_(e)) t^(2)` ....(ii)
Dividing (i) by (ii) , we get
`(x)/( d - x) = (m_(e ))/(m_(p)) rArr m_(p) x = m_(e ) d - m_(e )x`
`x = (m_(e )d)/(m_(e ) + m_(p))`