An electron (e,m) is projected into a uniform electric field E vertically downward between parallel plates at separation d, with velocity v0. The electron enters the electric field at a point midway between the plates. Find
(a) the magnitude of electric field if electron emerges from the electric field just at the edge of upper plate.
(b) the direction of the velocity of electron as it emerges from the electric field.
(c ) the equation of trajectory followed by electron.
The length of plates is L and consider only electric force.
This problem is similar to when a ball is thrown from the top of a tower horizontally in uniform gravational field , this is a case of two - dimensional motion.
Let the particle reaches to point P after time t.
x-direction (uniform motion):
vx=v0 ...(i)
x=uxt=v0t ....(ii)
y-direction (acceleration motion) :
vy=uy+ayt=eEmt ....(iii)
y=uyt+12ayt2=12eEmt2 ....(iv)
(a) When the paticle reaches to point A
x=v0t⇒L=v0t⇒t=Lv0
y=12eEmt2⇒d2=eE2m(Lv0)2⇒E=mv20deL2
(b) At A :
tanθ=vyvx=eEt/mv0=eELmv20
θ=tan−1(eELmv20)
where θ : angle made by the velocity of electron with initial direction of velocity.
(c ) To find trajectory, eleiminating t from (ii) and (iv)
y=12eEm(x2v0)2=eEx22mv0
This is the equation of parabola , hence trajectory of electron is parabolic.


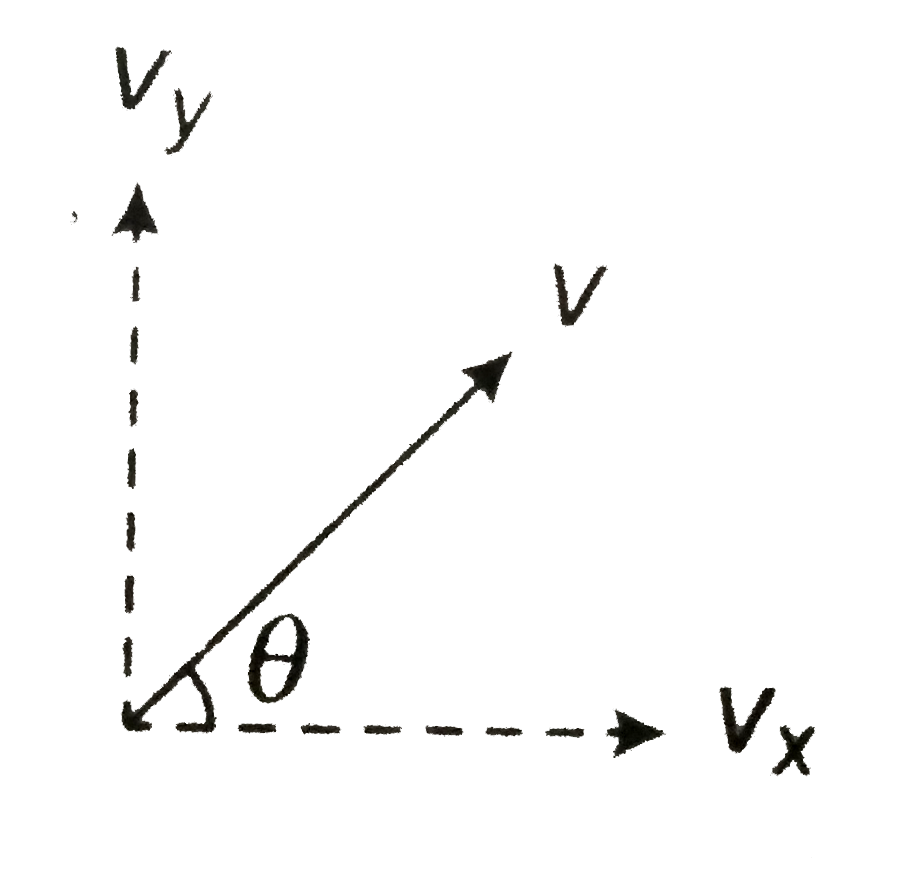
Topper's Solved these Questions
Similar Questions
An electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionAn electron is projected with an initial velocity of 107ms−1 into an electric field between two parallel plates 1 cm apart. The electron enters the field at a point midway between the plates. If the electron just misses the positivity charged plate as it emerges from the field, find the magnnitude of the electric density between the plates. (Length of each plate is 2 cm, mass of electron=9×10−31kg and charge of electron =1.6×10−19C)
View Solution
Knowledge Check
For uniform electric field, potential difference between the plate is
A1ε0QAdB1ε0AdQCε0QAdD1ε0QdAThe electric field (→E) between two parallel plates of a capacitor will be uniform if.
Athe plate separation (d) is equal to area of the plate (A)Bthe plate separation (d) greater when compared to area of the plate (A)Cthe plate separation (d) is less when compared to area of the plate (A)D2 (or) 3An electron enters in an electric field with its velocity in the direction of the electric lines of force. Then
AThe path of the electron will be a circleBThe path of the electron will be a parabolaCThe velocity of the electron will decreaseDThe velocity of the electron will increase
A uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plates with a
. speed v_(0)'. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionA uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan−1(eElμ2)]

View SolutionElectron beam enter an electric field normal to the field. Then their path in the electric field is .
View SolutionA uniform electric field E is created between two parallel charged plates as shown in figure . An electron enters the field symmetrically between the plates with a speed v0. The length of each plate is l. Find the angle of deviation of the path of the electron as it comes out of the field.

View Solution
