(a) Two protons are placed at separation d on a smooth surface. Find the speed of each proton when separation between them is doubled.
(b) An α-particle and a proton are placed at a separation d on a smooth surface.Find the speed of each when separation between them becomes infinite. (m: mass of proton , e: charge of proton.)
Video Solution
Text Solution
(A) Since external force is zero , momentum of system is conserved . The speed of each proton will be same.
Energy conservation between ① and ②
K1+U1=K2+U2
0+14π∈0.e.ed=12mv2+12mv2+14π∈0.e.e2d
mv2=14π∈0.e22d⇒v=√e28π∈0md
(b) By momentum conservation
0=−4mvα+mvp⇒v0=vp4
By energy conservation
K1+U1=K2+U2
0+14π∈0.2e.ed=12.4mv2α+12.mv2p+0
e22π∈0d=2m(vp4)2+12mv2p=58mv2p
vp=√4e25π∈0md,vα=vp4
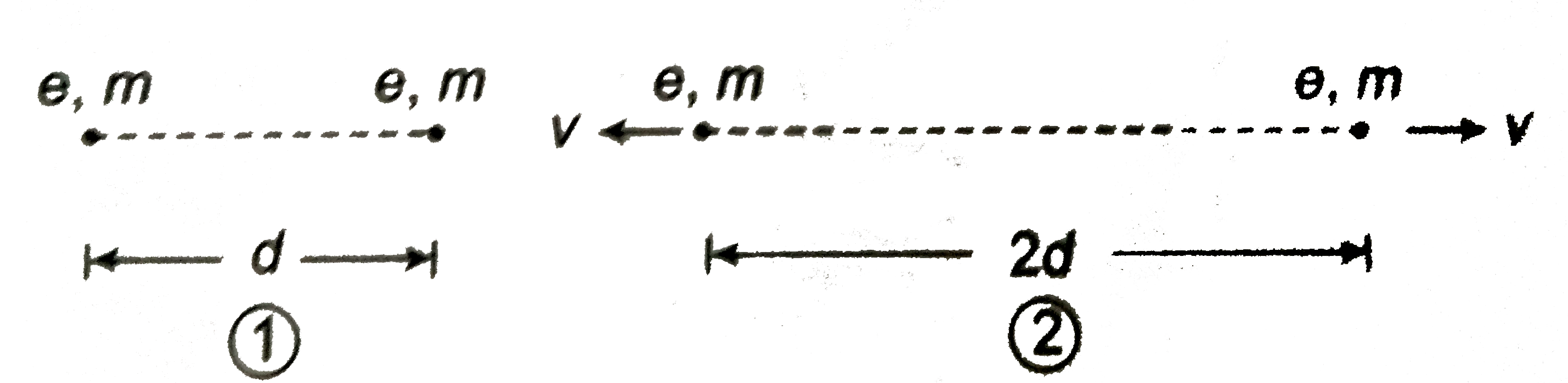
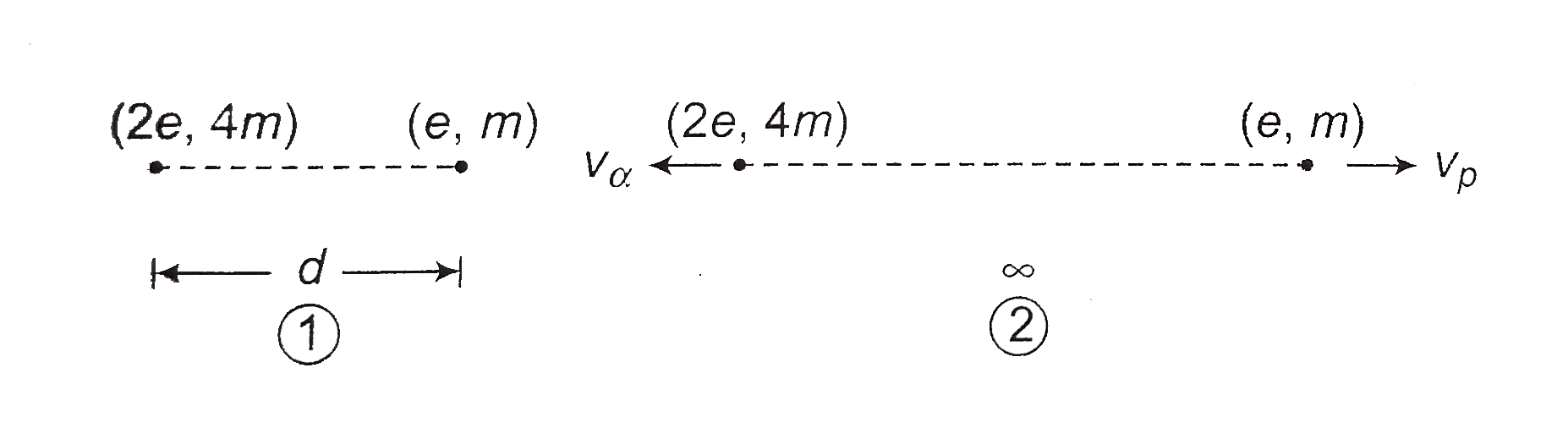
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A proton and α-particle are placed at separation d on a smooth surface . The ratio of their speed when separation becomes infinite will be
A4:1B2:1C1:4D1:2 - Question 2 - Select One
Two protons are kept at a separation of 50Å. Fn is the nuclear force and Fe is the electrostatic force between them, then
AFn>>FeBFn=FeCFn<<FeDFn≈Fe - Question 3 - Select One
In above question 1, find the speed of each speed of each particle, when the separation reduces to half its initial value
A√GmdB√2GmdC√Gm2dDNone of these
Two protons are separated by a distance R. What will be the speed of each proton when they reach infinity under their mutual repulsion?
View SolutionTwo protons are kept at a separation of 10nm. Let FnandFe be the nuclear force and the electromagnetic force between them.
View SolutionIf the area of each plate is A and the separation between them is d, then find the equivalent capacitance between P and Q
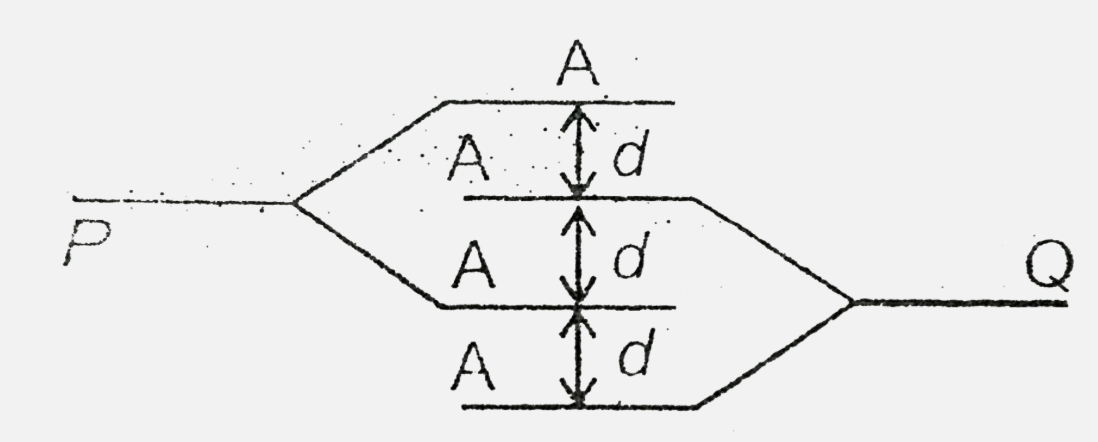 View Solution
View SolutionA proton and an electron are placed 1.6 cm apart in free speace. Find the magnitude and nature of electrostatic force between them.
View SolutionTwo particles of masses 1 kg and 2 kg are placed at a separation of 50 cm find out gravitational force between them
View Solution


