(a) A particle of mass $1 m g$ and having charges $1 μ C$ is moving in a magnetic field $\to B = 2 ˆ i + 3 ˆ j + k T$ , with velocity $\to v = 2 ˆ i + ˆ j - ˆ k m / sec$ . Find magnetic force in vector form and magnitude of acceleration.
(b) A magnetic field of $8 ˆ k T$ exerts a force $8 ˆ i + 6 ˆ j N$ on a particle having a charge $2 C$ and going in $x - y$ plane. Find the velocity of the particle.
( c) A particle is moving in a magnetic field $3 ˆ i + 4 ˆ j T$ and acceleration of particle is $λ ˆ i + 3 ˆ j m / {sec}^{2}$ . Find the value of $λ$ .
(d) When a proton has a velocity $b e c (v) = (2 ˆ i + 3 ˆ j) \times 10^{6} m / sec$ it experiences a force $\to F = (- 1.28 \times 10^{- 13} \to k) N$ . When its velocity is along the z-axis, it experiences a force along the x-axis. What is the magnetic field ?
(e) A circular loop of radius $20 c m$ carries a current of $10 A$ . An electron cross the plane of the loop with a speed of $2.0 \times 10^{6} m / sec$ . The direction of motion makes an angle centre. Find the magnitude of the magnetic force on the electron at the instant it crosses the plane.

Text Solution

Verified by Experts

(a) $m = 1 m g = 10^{- 6} k g, q = 1 μ C = 10^{- 6 C}$
$\to B = 2 ˆ i + 3 ˆ j + ˆ k T, \to v = 2 ˆ i + ˆ j - ˆ k m / sec$
$\to F = q \to v \times \to B = 10^{- 6} ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k 2 & 1 & - 1 2 & 3 & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣$
$\to a = \frac{\to F}{m} = \frac{10^{- 6}}{10^{- 6}} (4 ˆ i - 4 ˆ j + 4 ˆ k)$
$= 4 ˆ i - 4 ˆ j + 4 ˆ k m / {sec}^{2}$
$| \to a | = a = 4 \sqrt{3} m / {sec}^{2}$
(b) The particle is moving in $x - y$ plane, hence its velocity
$\to v = v_{x} ˆ i + v_{y} ˆ j m / sec$
$q = 2 C, \to B = 8 ˆ k T, \to F = 8 ˆ i + 6 ˆ j N$
$\to F = q \to v \times \to B = 2 ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k v_{x} & v_{y} & 0 0 & 0 & 8 \end{matrix} ∣ ∣ ∣ ∣ ∣$
$= 2 [8 v_{y} ˆ i - 16 v_{x} ˆ j]$
$8 ˆ i + 6 ˆ j = 16 v_{y} ˆ i - 16 v_{x} ˆ j$
Comparing coefficient of $ˆ i$ and $ˆ j$
$16 v_{y} = 8 \Rightarrow v_{y} = \frac{1}{2}$
$- 16 v_{x} = 6 \Rightarrow v_{x} = - \frac{3}{8}$
$\to v = v_{x} ˆ i + v_{y} ˆ j = - \frac{3}{8} ˆ i + \frac{1}{2} ˆ j m / sec$
( c) $\to B = 3 ˆ i + 4 ˆ j T, \to a = λ ˆ i + 3 ˆ j m / {sec}^{2}$
Since $\to F = q \to v \times \to B, \to F$ is $⊥^{a r}$ to $\to v$ as wll as $\to B$
$\to F = m \to a$ , hence $\to a$ is $⊥^{a r}$ to $\to B$
The dot product of perpendicular vectors is zero.
$\to B . \to a = 0$
$(3 ˆ i + 4 ˆ j) . (λ ˆ i + 3 ˆ j) = 0$
$λ = - 4$
(d) $\to v = (2 ˆ i + 3 ˆ j) \times 10^{6} m / sec, \to F = - (1.28 \times 10^{- 13} ˆ k)$
Since $\to F$ is $⊥^{a r}$ to $\to B, \to B$ should be in $x - y$ plane
Let $\to B = B_{x} ˆ i + B_{y} ˆ j$
$\to F = q \to v \times \to B = (1.6 \times 10^{- 9}) ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k 2 \times 10^{6} & 3 \times 10^{6} & 0 B_{x} & B_{y} & 0 \end{matrix} ∣ ∣ ∣ ∣ ∣$
$- (1.28 \times 10^{- 13}) ˆ k = (1.6 \times 10^{- 19} \times 10^{6}) [2 B_{y} - 3 B_{x}] ˆ k$
$2 B_{y} - 3 B_{x} = 0.8$ ...(i)
Let $\to v = v_{0} ˆ k, \to F = F_{0} ˆ i$
$\to F = q \to v \times \to B$
$F_{0} ˆ i = q (v_{0} ˆ k) \times (B_{x} ˆ i + B_{y} ˆ j)$
$= q v_{0} [B_{x} ˆ j - B_{y} ˆ i]$
$= q v_{0} B_{x} ˆ i - q v_{0} B_{y} ˆ i$
Comparing coefficient of $j$ : $q v_{0} B_{x} = 0 \Rightarrow B_{x} = 0$
$2 B_{y} - 3 B_{x} = 0.8 \Rightarrow B_{y} = 0.4$
$\to B = 0.4 ˆ j T$
(e)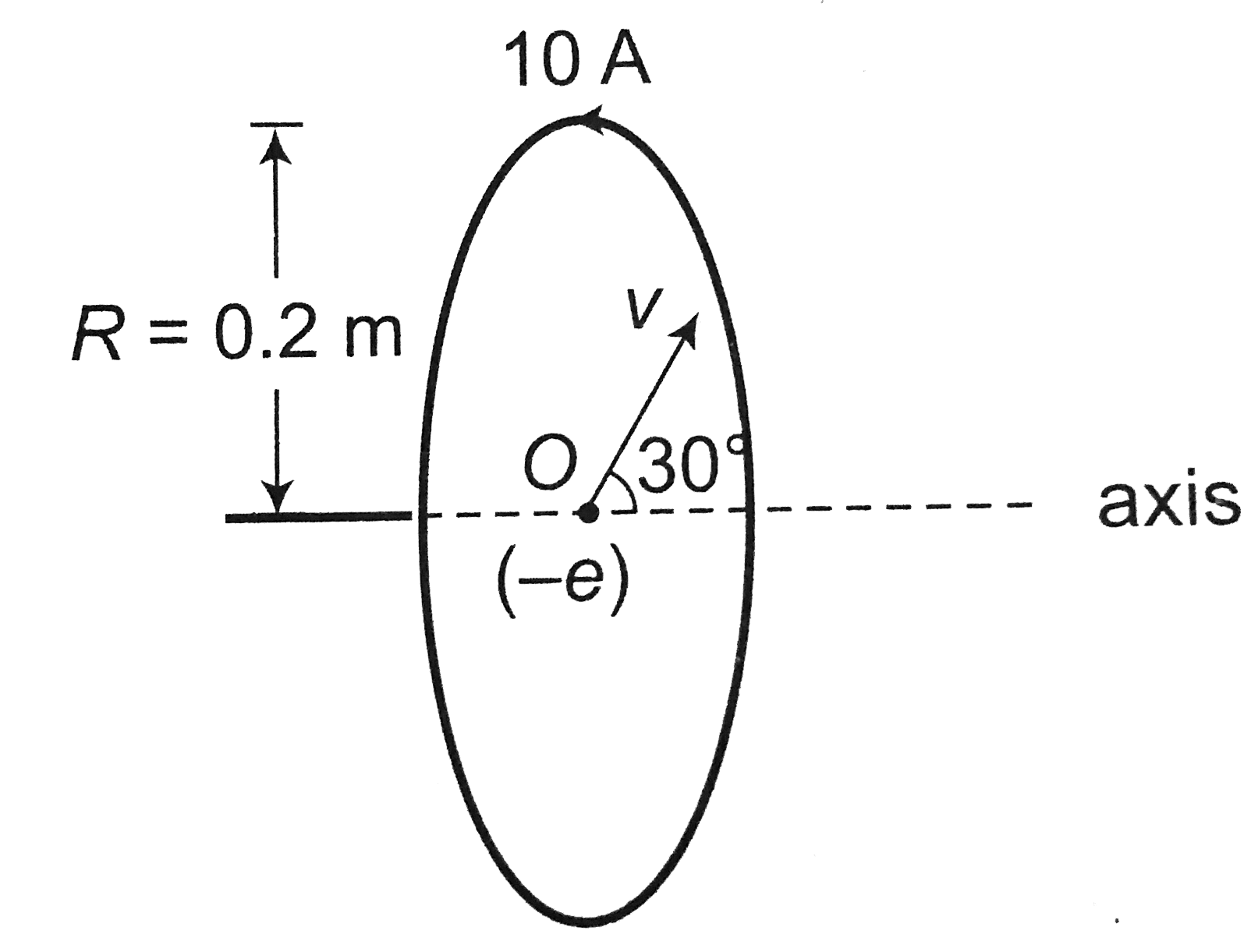
Magnetic field centre of loop
$B = \frac{μ_{0} i}{2 R} = \frac{(4 π \times 10^{- 7}) (10)}{2 \times 0.2} = π \times 10^{- 5} T$ , along x-axis
$\to B = π \times 10^{- 5} ˆ i T$
Velocity of electron, $| \to v | = v = 2 \times 10^{6} m / sec$
$\to v = v {cos 30}^{\circ} ˆ i + v {sin 30}^{\circ} ˆ j = (\sqrt{3} ˆ i + ˆ j) \times 10^{6} m / sec$
$\to F = q \to v \times \to B = (- 1.6 \times 10^{- 19}) ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k \sqrt{3} \times 10^{6} & 10^{6} & 0 10^{- 5} π & 0 & 0 \end{matrix} ∣ ∣ ∣ ∣ ∣$
$= (1.6 \times 10^{- 19}) (10^{6}) (10^{- 5} π) ˆ k$
$= 1.6 π \times 10^{- 18} ˆ k N$
$∣ ∣ \to F ∣ ∣ = 1.6 π \times 10^{- 18} N$

Updated on:21/07/2023