A wire loop ABCDE carrying a current I is placed in the x−y plane as shown in the figure. A particle of mass m and charge q is projected from origin with velocity
→V=V0√2(ˆi+ˆj)m/sec.
(a) Find the instaneous acceleration
(b) If an external magnetic field →B=B0ˆi is applied, find the force and torque acting on the loop due to this field.

(a) 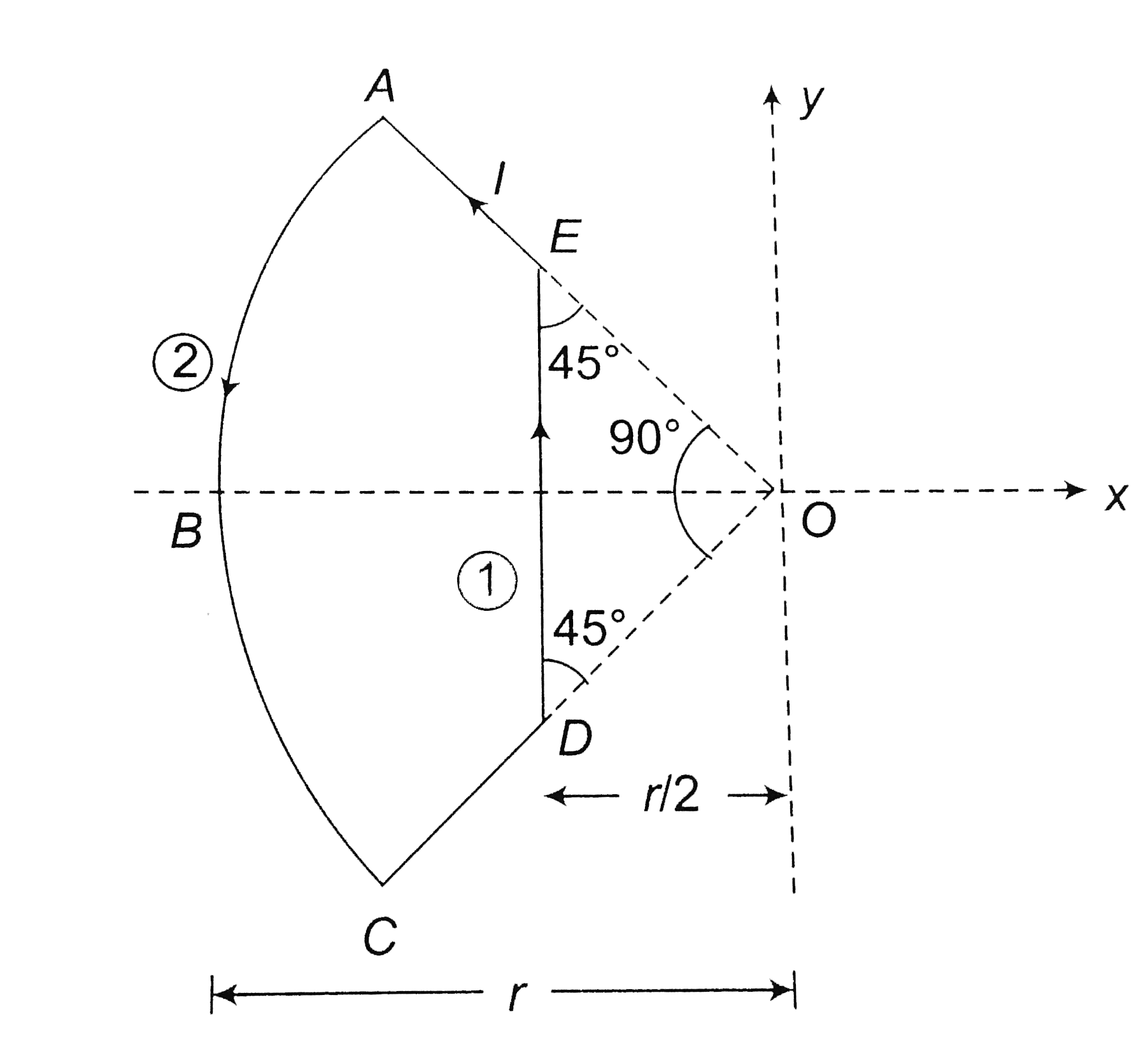
Magnetic field at O due to loop ABCDE
→B1=μ0I4πr2(cos45∘+cos45∘)(−ˆk)
=−μ0I2πr.2.1√2ˆk
=−μ0I√2πrˆk
→B2=μ0I2r.90∘360∘ˆk=μ0I8rˆk
B0=→B1+→B2=μ0Ir(18−1√2π)ˆk
Magnetic force on charged particle at O
→F=q→V×→B
=q[V0√2(ˆi+ˆj)]×[μ0Ir(18−1√2π)ˆk]
=μqV0I√2r(18−1√2π)[(ˆi+ˆj)׈k]
=μqV0I√2r(18−1√2π)(−ˆj+ˆi)
Acceleration
→a=→Fm
=μqV0I√2m(π−4√28π)(ˆi−ˆj)
=μqV0I8√2πmr(π−4√2)(ˆi−ˆj)
(b) Now external magnetic field →B=B0ˆi is applied. Net magnetic force on loop =0 (when a closed loop carrying single current is placed in uniform magnetic field, net magnetic force on loop is zero, whatever the shape of loop)
Area of loop =πr24−12r.12=r2(π4−14)
Magnetic moment of loop →M=IA=Ir24(π−1)ˆk
Torque acting on loop
→τ=→M×→B=B0Ir24(π−1)[ˆk׈i]
=B0Ir2(π−1)4ˆj
Topper's Solved these Questions
Similar Questions
A wire loop carrying I is placed in the x−yplane as shown in fig.
(a) If a particle with charge +Q and mass m is placed at the centre P and given a velocity →v along NP(see figure), find its instantaneous acceleration.
( b) If an external uniform magnetic induction field →B=Bˆi is applied , find the force and the torque acting on the loop due to this field.
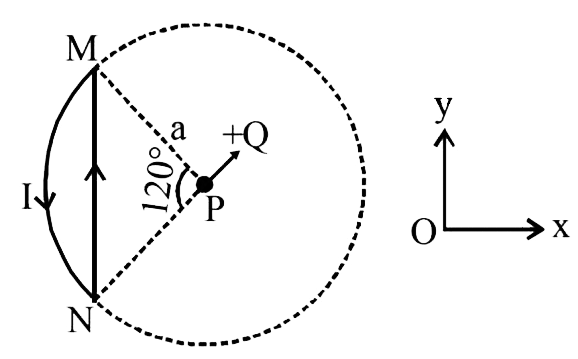
View SolutionA wire loop carrying I is placed in the x−yplane as shown in fig.
(a) If a particle with charge +Q and mass m is placed at the centre P and given a velocity →v along NP(see figure), find its instantaneous acceleration.
( b) If an external uniform magnetic induction field →B=Bˆi is applied , find the force and the torque acting on the loop due to this field.

View Solution
Knowledge Check
A magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
A175ˆkN−mB150ˆkN−mC75ˆkN−mD25√37ˆkN−mAn electron is moving with a velocity (2ˆi+2ˆj)m/s is an electric field of intensity →E=ˆi+2ˆj−8ˆkV/m and a magnetic field of →B=(2ˆj+3ˆk) tesla. The magnitude of force on the electron is
A14.4×10−19NB9×10−19NC11.2×10−19ND6.4×10−19NA magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
A175ˆk Nm,B75ˆiNmC150ˆiNmD25√37ˆiNm,
A wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
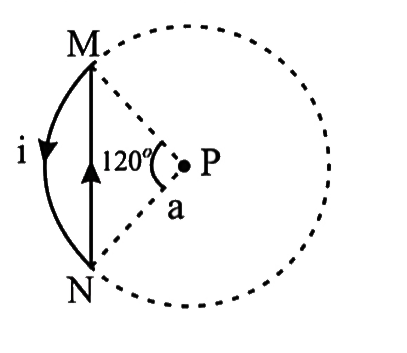
View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is

View SolutionA wire loop carrying a current I is placed in the x-y plane. (a) If a particle with charge +Q and mass m is placed at the center P and given a velocity →v along NP, find its acceleration. (b) if an external uniform magnetic induction →B=Bˆi is applied, find the force and the torque acting on the top due to this field.
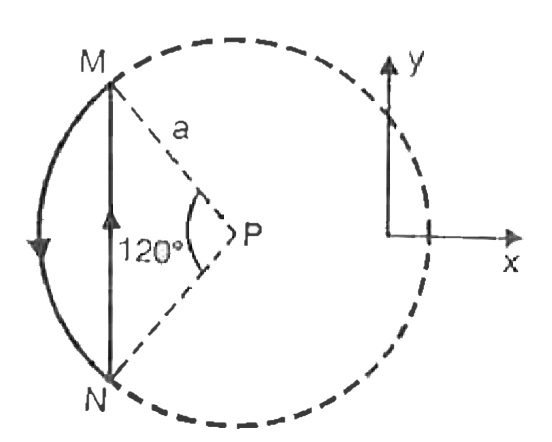
View SolutionA particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
View Solution
