A radioactive source, in the form of a metallic sphere of radius 10−2m emits β−particles at the rate of 5×1010 particles per second. The source is electrically insulated. How long will it take for its potential to be raised by 2V, assuming that 40% of the emitted β−particles escape the source.
β-particles i.e. electron
V=14π∈0.qr=9×10910−2q=9×1011q
2=9×1011q
q=29×10−11C
where q: charge acquired by sphere.
Number of β-particles emitted by source =5×1010/sec
40% of this =0.4×5×1010/sec=2×1010/sec
q=net
29×10−11=2×1010×1.6×10−19t
t=10−29×1.6
Topper's Solved these Questions
Similar Questions
A radioavtive source in the form of a metal sphere of daimeter 10−3 m emits β-particles at a constant rate of 6.25×1010 particles per second. If the source is electrically insulated, how long will it take for its potential to rise by 1.0V, assuming that 80% of the emitted β-particles escape the socurce?
View SolutionCalculate t3/2 for Am241 in years given that it emits 1.2×1011α-particles per gram per second
View Solution
Knowledge Check
- Question 1 - Select One
A radioactive source in the form of a metal sphere of diameter 3.2×10^ −3 m emits β-particle at a constant rate of 6.25×10^ 10 particle/sec. The source is electrically insulated and all the β-particle are emitted from the surface. The potential of the sphere will rise to 1 V in time
A180μsB90μsC18μsD9μs - Question 2 - Select One
A 16μF capacitor , initially charged to 5 V, is started charging at t=0 by a source at the rate of 40tμCs−1. How long will it take to raise its potential to 10 V?
A1 sB2 sC3 sDnone of these - Question 3 - Select One
A radioactive substance emits n beat particles in the first 2 s and 0.5 n beta particles in the next 2 s. The mean life of the sample is
A4 sB2 sC2(1n2)D2 (1n 2) s
A monochromatic light source of frequency 6×1014Hz is emitting energy at the rate 2×10−3J/s. Calculate the number of photons emitted per seconds by source.
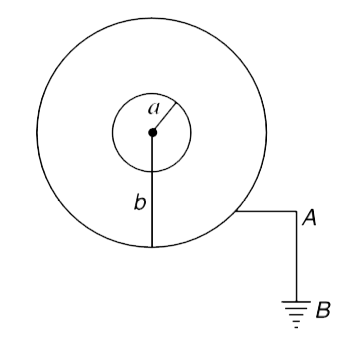
View SolutionA β active radioactive source is in the form of a conducting sphere of radius a. it is surrounded by a concentric conducting shell of radius b(>a). The shell is grounded. β particles are emitted with kinetic energy ranging from E1 to E2(>E1)
(a) Find the maximum potential that will the acquired by the sphere of radius a.
(b) Find the total charge that will flow through the grounding wire AB.
(c) Find the final maximum charge on the outer sphre
 View Solution
View SolutionA particle of mass 1 g and charge 2.5×10−4C is released from rest in an electric field of 1.2×104NC−1 (a) Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis? (b) How long will it take for the particle to travel a distance of 40 cm? (c) What will be the speed of the particle after travelling this destance? (d) how much is the work done by electric force on the particle during this period?
View SolutionAn electric gum emits 2.0×1016 electrons per second. What electric current does this correspond to ?
View SolutionThe atomic weight of radius is 226. It is observed that 3.67×1010 α−particles are emitted per second from one gram of radium. Calculate in years the half period of radium.
View Solution

