(ii)The radical axis bisects the common tangents of two circles.
Step by step video & image solution for (ii)The radical axis bisects the common tangents of two circles. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Two circle touch each other externally at the point (0,k) and y-axis is the common tangent to these circles. Centres of these circle lie on the line
Ax=kBy=kCx+y=kDx−y=kT is a point on the common tangents at P of two circles and if TA and TB are respectively the other tangents at A and B to the two circles drawn from the point T then
ATA=2TBBTA=TBCTA=12TBD3TA=TBR and r are the radii of two circles (R > r). If the distance between the centres of the two circles be d, then length of common tangent of two circles is
A√r2−d2B√d2−(R−r2)C√(R−r)2−d2D√R2−d2
Two circles of radius 1 and 4 touch each other externally. Another circle of radius r touches both circles externally and also one direct common tangent of the two circles. Then [1r]=
View Solution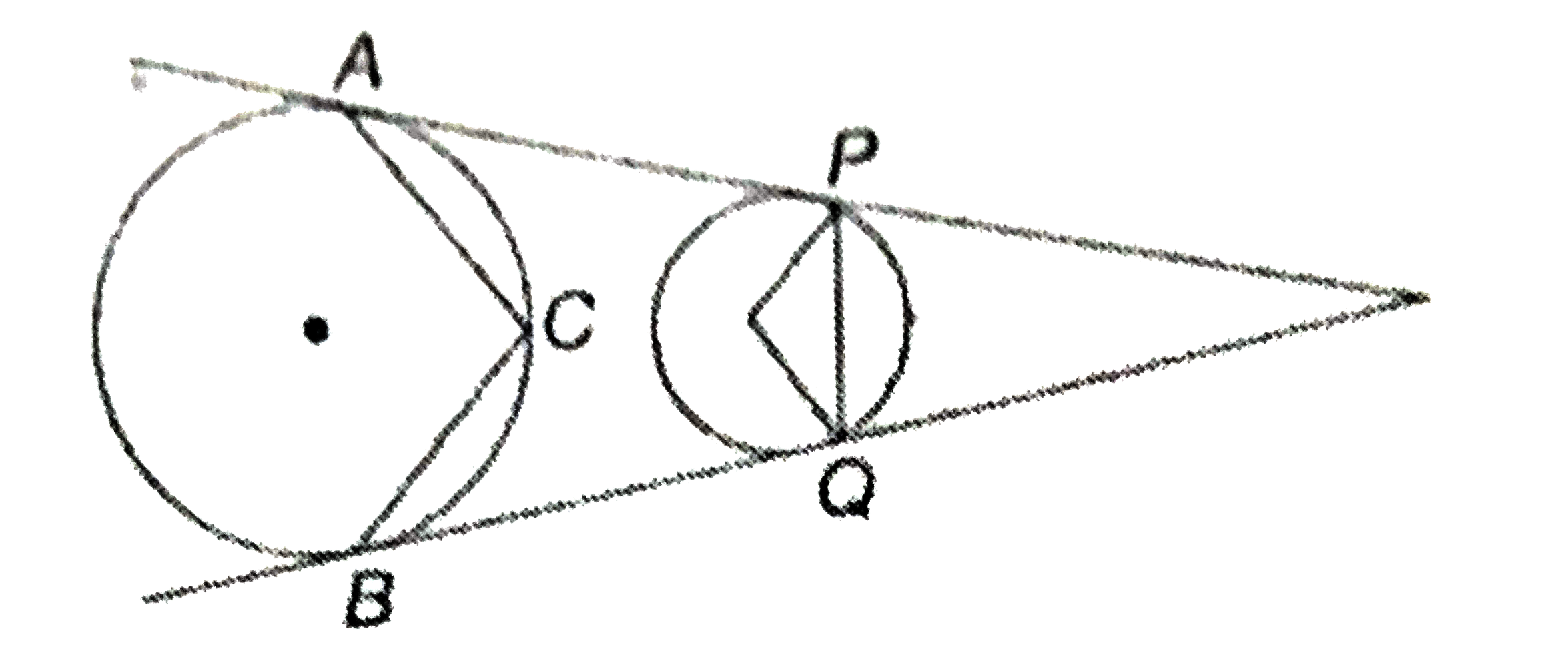
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View SolutionConsider two statements S1 && S2 as s1: Radical Axis is identical to common chord of two circles which are intersecting S2: Radical Axis is locus of all such points such that lengths of tangents drawn from it to two circles are equal
View SolutionR and r are the radius of two circles (R>r). If the distance between the centre of the two circles be d, then length of common tangent of two circles is
View SolutionTwo circles touch each other externally at P. AB is a direct common tangent to the two circles, A and B are point of contact and ∠PAB=35∘. Then ∠ABP is
View Solution
