A ray of light makes an angle of 10∘ with the horizontal and strikes a plane mirror which is inclined at an angle θ to the horizontal. The angle θ for which the reflected ray becomes vertical, is
40
50∘
80∘
100∘
The correct Answer is:A
To solve the problem, we need to analyze the situation step by step using the laws of reflection.
Step 1: Understand the angles involved
- The ray of light makes an angle of 10∘ with the horizontal. This angle is the angle of incidence (i).
- The mirror is inclined at an angle θ to the horizontal.
Step 2: Determine the angle of incidence with respect to the mirror
- The angle of incidence (i) with respect to the normal to the mirror is given by:
i=90∘−(θ+10∘)
- This is because the angle of incidence is measured from the normal, which is perpendicular to the surface of the mirror.
Step 3: Apply the law of reflection
- According to the law of reflection, the angle of reflection (r) is equal to the angle of incidence (i):
r=i
- Therefore, we can write:
r=90∘−(θ+10∘)
Step 4: Determine the condition for the reflected ray to be vertical
- For the reflected ray to be vertical, the angle of reflection must be 90∘:
r=90∘
- Substituting this into the equation from Step 3, we get:
90∘=90∘−(θ+10∘)
Step 5: Solve for θ
- Rearranging the equation gives:
θ+10∘=0
- Therefore, we find:
θ=−10∘
Conclusion
The angle θ for which the reflected ray becomes vertical is −10∘.
---
- The ray of light makes an angle of 10∘ with the horizontal. This angle is the angle of incidence (i).
- The mirror is inclined at an angle θ to the horizontal.
- The angle of incidence (i) with respect to the normal to the mirror is given by:
i=90∘−(θ+10∘)
- This is because the angle of incidence is measured from the normal, which is perpendicular to the surface of the mirror.
- According to the law of reflection, the angle of reflection (r) is equal to the angle of incidence (i):
r=i
- Therefore, we can write:
r=90∘−(θ+10∘)
- For the reflected ray to be vertical, the angle of reflection must be 90∘:
r=90∘
- Substituting this into the equation from Step 3, we get:
90∘=90∘−(θ+10∘)
- Rearranging the equation gives:
θ+10∘=0
- Therefore, we find:
θ=−10∘
The angle θ for which the reflected ray becomes vertical is −10∘.
Topper's Solved these Questions
- REFLECTION OF LIGHTBook:CP SINGHChapter:REFLECTION OF LIGHTExercise:EXERCISES
Explore 67 Videos
- PHOTOELECTRIC EFFECTBook:CP SINGHChapter:PHOTOELECTRIC EFFECTExercise:EXERCISES
Explore 73 Videos
- REFRACTION AT SPHERICAL SURFACESBook:CP SINGHChapter:REFRACTION AT SPHERICAL SURFACESExercise:EXERCISES
Explore 105 Videos
Similar Questions
A ray of light making an angle 50∘ with the horizontal is incident on a plane mirror, which itself is inclined to the horizontal at an angle 10∘ as shown in the figure .Determine the angle made by the reflected ray with the horizontal _____

View SolutionAn incident ray strikes a plane mirror at an angle of 15∘ with the mirror. The angle between the incident ray and reflected ray is
View Solution
Knowledge Check
A mirror is inclined at an angle of θ with the horizontal. If a ray light is incident at an angle θ as shown , then the angle made by reflected ray with the horizontal is
_E01_002_Q01.png) AθB2θCθ2Dzero
AθB2θCθ2DzeroAn incident ray strikes a plane mirror at an angle of 15∘ with the mirror. The angle between the reflected ray and the mirror is
A15∘B30∘C75∘Dnone of theseA ray of light is incident at an ∠ of 30∘ on a plane mirror M1. Another mirror M2 is inclined at angle θ to M1. What is the value of angle θ so light reflected from M2 is parallel to M1.
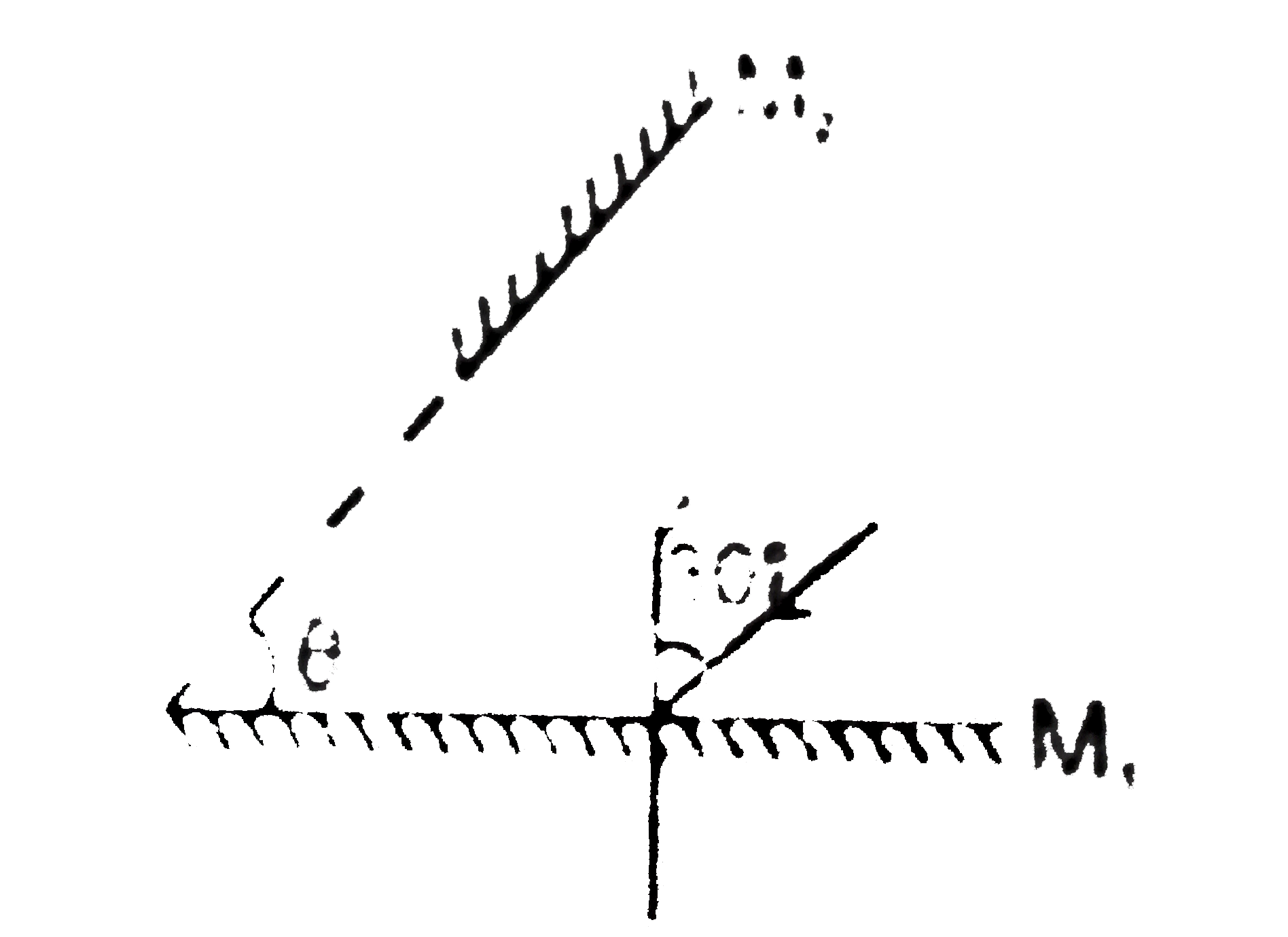 .A60∘B75∘C67.5∘Dnone of these
.A60∘B75∘C67.5∘Dnone of these
When a mirror is rotated by a angle θ , the reflected ray will rotated by
View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray of light is incident at an angle in incidence θ then the reflected ray will make the angle with horizontal, is
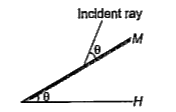
View Solutionplane mirror makes an angle of 30∘ with horizontal. If a vertical ray strikes the mirror, find the angle between mirror and reflected ray
View SolutionA plane mirror makes an angle of 30∘ with horizontal. If a vertical ray strikes mirror, find the angle between mirror and reflected ray
View SolutionA ray of light is incident at an angle of 35∘ on a plane mirror. What is angle θ ?

View Solution