Consider a tin can of height h as shown in the figure. A coin lies on the botttom at the centre. From the position shown you can barely see the far side of the bottom of the can. When the can is slowly filled with water of refractive index , coin is just visible when the can is full. Show that the ratio of the height to radius is

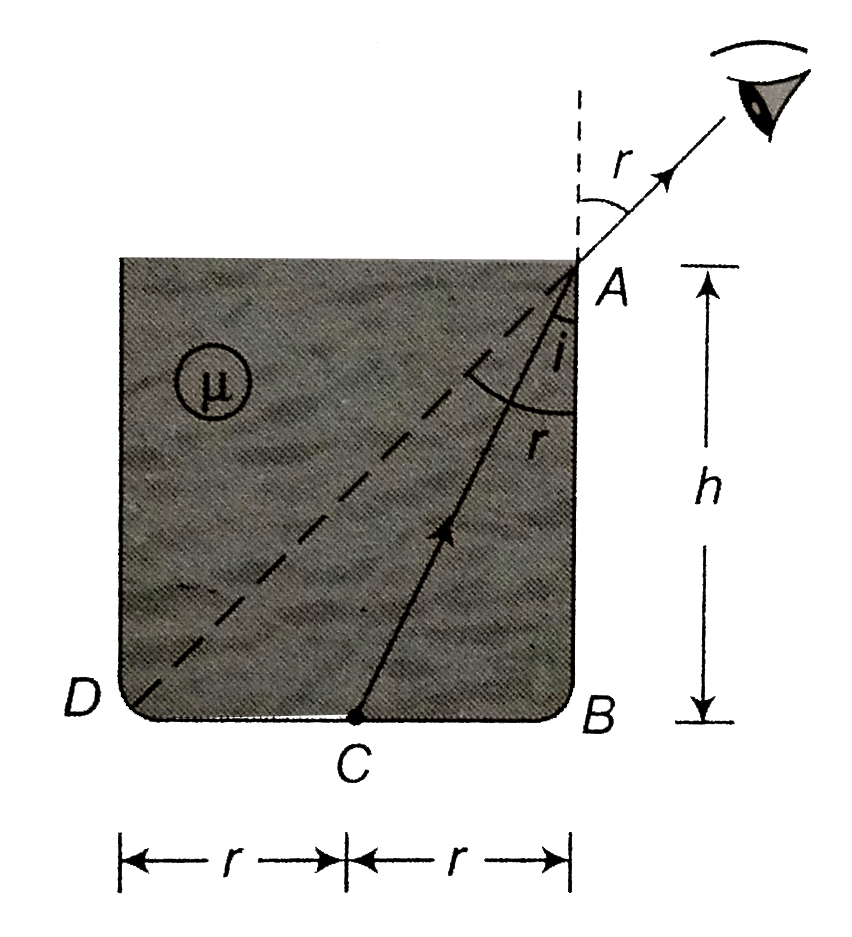
When vessel is filled with water, ray coming from coin, after refraction goes along inclined line of vision and hence the coin becomes visible.
By Snell's law,
Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises140videos
SEMICONDUCTORS
Similar Questions
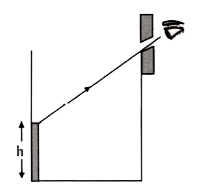
A rod of height h is palced in a beaker of same radius. The height of the beaker is 3 times its radius. An observer sees the top end of the rod through a pin hole. When the beaker is filled with a liquid of refractive index √μ upto a height 2h, he can see the lower end of the rod. Find the value of μ
 View Solution
View SolutionConsider the situation shown in figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) up of a bottom formed by the mirror.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A glass beaker has diameter 4cm wide at the bottom. An observer observes the edge of bottom when beaker is empty as shown in figure. When the beaker is completely filled with liquid of refractive index n=√5/2, he can just see the centre of bottom, then the height of glass beaker is :
 A4cmB√5/2cmC16cmDNone of these
A4cmB√5/2cmC16cmDNone of these - Question 2 - Select One
What can you infer about the structures shown in figure?
 AThey are homologous structures.BThey are vestigial structures.CThey are analogous structures.DThey have nothing to do with each other.
AThey are homologous structures.BThey are vestigial structures.CThey are analogous structures.DThey have nothing to do with each other. - Question 3 - Select One
For an eye kept at a depth h inside water is refractive index μ, and viewed outside, the radius of circle through which the outer objects can be seen will be
Ah√μ2−1BhμCh√μ2+1D(√μ2−1μ)h
Consider the situation shown in Figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) upto a height d. Find the position of the image of bottom formed by the mirror.
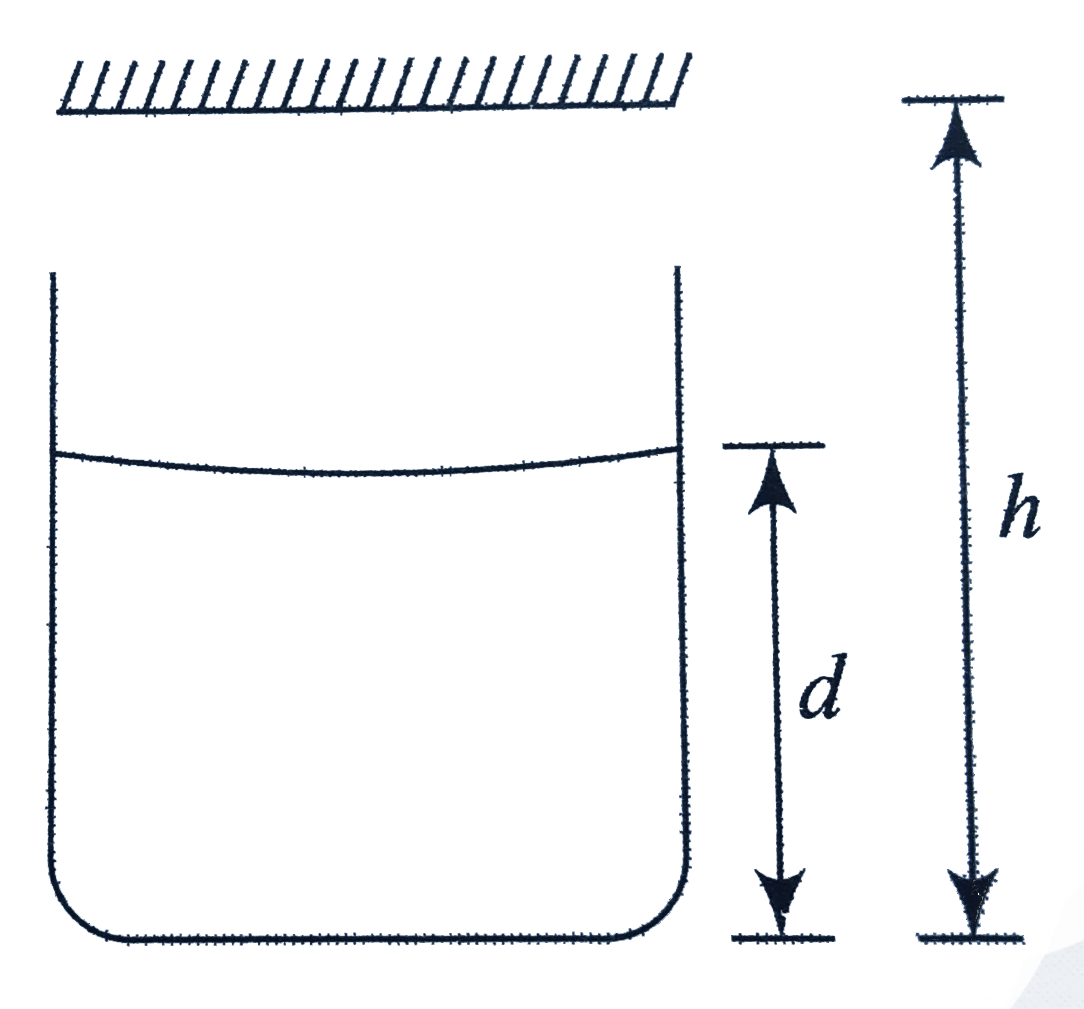 View Solution
View SolutionThe moon and the planets do not twinkle. Why? Can you see the stars twinkling when observed from the moon? Why?
View SolutionShow the Part of the image which man can see in the mirror as shown in the figure.
 View Solution
View SolutionA beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K oil is μ2.
View SolutionA pipe can fill a tank in 20 h. due to a leak in the bottom , it is filled in 40 h .if the tank is full how much time will the leak take to empty it ?
View Solution

