A bulb is placed at a depth of 2√7cm in water and a floating opaque disc is placed over the bulb so that the bulb is not visible from the surface. What is the minimum diameter of the disc?
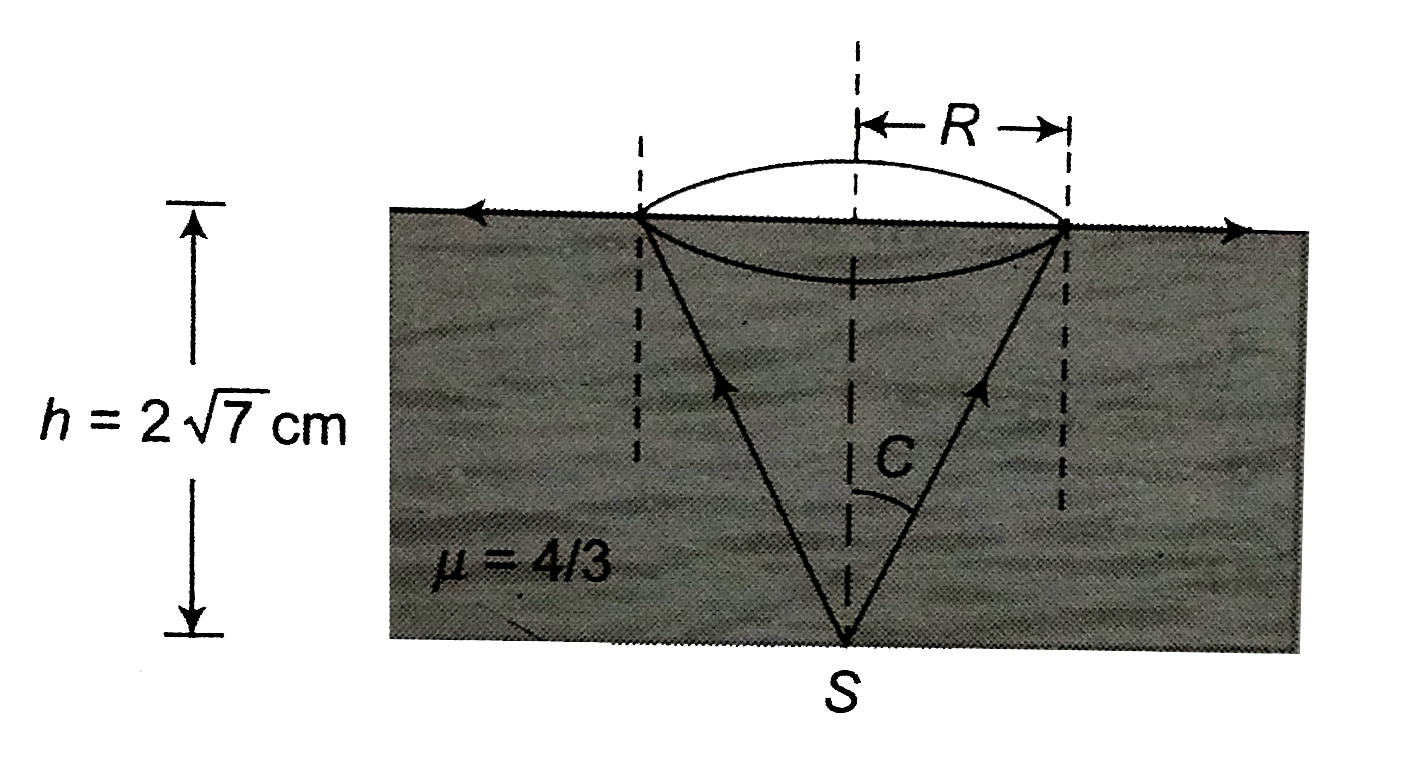
R=h√μ2−1=2√7√(43)2−1
=2√7√73=6cm
Diameter of disc =2R=12cm
Topper's Solved these Questions
- REFRACTION OF LIGHT BY PLANE SURFACESBook:CP SINGHChapter:REFRACTION OF LIGHT BY PLANE SURFACESExercise:Exercises
Explore 110 Videos
- REFRACTION AT SPHERICAL SURFACESBook:CP SINGHChapter:REFRACTION AT SPHERICAL SURFACESExercise:EXERCISES
Explore 105 Videos
- SEMICONDUCTORSBook:CP SINGHChapter:SEMICONDUCTORSExercise:Exercises
Explore 140 Videos
Similar Questions
An isotropic point source is placed at a depth h below the water surface. A floating opaque disc is placed on the surface of water so that the source is not visible from the surface. What is the minimum radius of the disc? Take refractive index of water=μ.
View SolutionIn a tank filled with a liquid of refractive index 5/3, a point source of light is placed 2m below the surface of water. To cut off all light coming out of water from the source, what should be the minimum diameter of a disc, which should be placed over the source on the surface of water ?
View Solution
Knowledge Check
A point source of light is placed at a depth of h below the surface of water of refractive index μ.A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface . The minimum diameter of the disc is
A2h(μ2−1)12B2h(μ2−1)12Ch2(μ2−1)12Dh(μ2−1)12A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2A point source of light is placed at the bottom of a vessel which is filled with water of refractive index μ to a height h. If a floating opaque disc has to be placed exactly above it so that the source is invisible from above, the radius of the disc should be-
Ah√μ−1Bh√μ2−1Chμ2−1Dμh√μ2−1
A 100 W light bulb is placed at the centre of a spherical chamber of radius 20cm. Assume that 60% of the energy supplied to the bulb is converted into light and that the surface of the chamber is perfectly absorbing. Find the pressure exerted by the light on the surface of the chamber.
View SolutionA small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. [Consider the bulb to be a point source]
View SolutionA disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionRefractive index of water is 5/3. A light source is placed in water at a depth of 4m. Then what must be the minimum radius of disc placed on water surface so that the light of source can be stopped?
View SolutionA disc rotates at 60rev/min around a vertical axis.A body lies on the disc at the distance of 20cm from the axis of rotation.What should be the minimum value of coefficient of friction between the body and the disc,so that the body will not slide off the disc
View Solution