Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
n>√2
n=1
n=1.1
n=1.3
The correct Answer is:A
To solve the problem of determining the minimum refractive index n of a transparent rod such that light entering it will not exit through its lateral face, we can follow these steps:
Step 1: Understand Total Internal Reflection
When light travels from a medium of higher refractive index to a medium of lower refractive index, it can undergo total internal reflection if the angle of incidence exceeds a certain critical angle. For the light to remain inside the rod, we need to ensure that total internal reflection occurs at the lateral surface of the rod.
Step 2: Define the Refractive Indices
Let:
- The refractive index of air (outside the rod) be n1=1.
- The refractive index of the rod be n.
Step 3: Apply Snell's Law
At the interface where light enters the rod, Snell's law states:
n1sin(θ1)=nsin(θ2)
Where:
- θ1 is the angle of incidence in air.
- θ2 is the angle of refraction in the rod.
Step 4: Determine Critical Angle for Total Internal Reflection
For total internal reflection to occur at the lateral surface of the rod, the angle of incidence θ2 must be greater than the critical angle θc. The critical angle can be given by:
sin(θc)=n1n
Thus, the critical angle is:
θc=arcsin(n1n)=arcsin(1n)
Step 5: Condition for Total Internal Reflection
For total internal reflection to occur, the angle of incidence θ2 must be greater than θc:
θ2>θc
This means that the angle θ2 must be such that:
sin(θ2)>1n
Step 6: Maximum Angle of Incidence
The maximum angle of incidence θ1 at which light can enter the rod is 90∘. Therefore, at this angle:
sin(θ1)=1
Substituting into Snell's law gives:
1⋅1=nsin(θ2)⟹sin(θ2)=1n
Step 7: Ensure Total Internal Reflection
To ensure that light does not exit the rod, we need:
sin(θ2)≥sin(θc)⟹1n≥1n⟹n≥√2
Conclusion
Thus, for the light to remain inside the rod without exiting through the lateral face, the refractive index n of the rod must be greater than √2.
Final Answer
The refractive index n must be greater than √2.
---
When light travels from a medium of higher refractive index to a medium of lower refractive index, it can undergo total internal reflection if the angle of incidence exceeds a certain critical angle. For the light to remain inside the rod, we need to ensure that total internal reflection occurs at the lateral surface of the rod.
Let:
- The refractive index of air (outside the rod) be n1=1.
- The refractive index of the rod be n.
At the interface where light enters the rod, Snell's law states:
n1sin(θ1)=nsin(θ2)
Where:
- θ1 is the angle of incidence in air.
- θ2 is the angle of refraction in the rod.
For total internal reflection to occur at the lateral surface of the rod, the angle of incidence θ2 must be greater than the critical angle θc. The critical angle can be given by:
sin(θc)=n1n
Thus, the critical angle is:
θc=arcsin(n1n)=arcsin(1n)
For total internal reflection to occur, the angle of incidence θ2 must be greater than θc:
θ2>θc
This means that the angle θ2 must be such that:
sin(θ2)>1n
The maximum angle of incidence θ1 at which light can enter the rod is 90∘. Therefore, at this angle:
sin(θ1)=1
Substituting into Snell's law gives:
1⋅1=nsin(θ2)⟹sin(θ2)=1n
To ensure that light does not exit the rod, we need:
sin(θ2)≥sin(θc)⟹1n≥1n⟹n≥√2
Thus, for the light to remain inside the rod without exiting through the lateral face, the refractive index n of the rod must be greater than √2.
The refractive index n must be greater than √2.
Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises140videos
SEMICONDUCTORS
Similar Questions
Light is incident at an angle i on one planer end of a transparent cylinderical rod of refractive index μ. Find the least value of μ so that the light entering the rod does not emerge from the curved surface of the rod irrespective of the value of i.
 View Solution
View SolutionLight is incident at an angle α on one planar end of a transparent cylindrical rod of refractive index μ. Determine the least value of μ so that the light entering the rod does not emerge from the curved surface of rod irrespective of the value of α
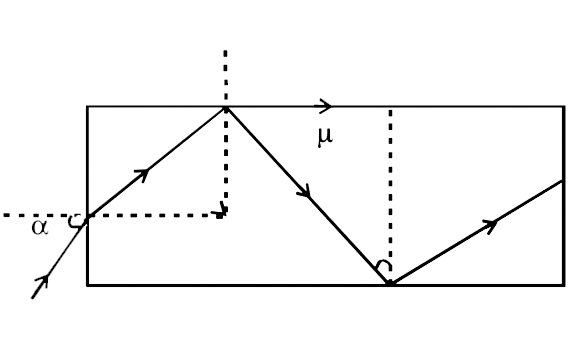 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Light enters at an angle of incidance in a tranjsparent road of refractve index μ. for what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidance ?
Aμ>√2Bμ=1Cμ=1.1Dμ=1.3 - Question 2 - Select One
A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3 - Question 3 - Select One
A ray of light is incident at an angle of 60∘ on the face of a prism with an angle of 60∘. Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
A1.414B1.623C1.524D1.732
A thin prism of refracting angle 2∘ deviates an incident ray through an angle of 1∘.Find the value of refractive index of material of prism.
View SolutionA ray of light is incident on a transparent plate of a material of refractive index √3 at the polarising angle. Find the angle of refraction.
View SolutionA ray of light falls on a material body at an incident angle 60∘ and refracted at angle 30∘.
What is the refractive index of the material?View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionFind the lateral shift produced in a ray of light incident on a material of refractive index 1.45 at an angle of 30∘. The thickness of the material is 5 cm.
View Solution

