The elastic potential enegry of a stretched spring is given by . Where is the displacement in meter and and is in joule, then the force constant of the spring is
50 Nm
100 Nm
The correct Answer is:B
, , compare equation (1) and (2) to find .
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- II (C.W)
Explore 68 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- III (C.W)
Explore 50 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:C.U.Q-Key
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
Knowledge Check
The spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
A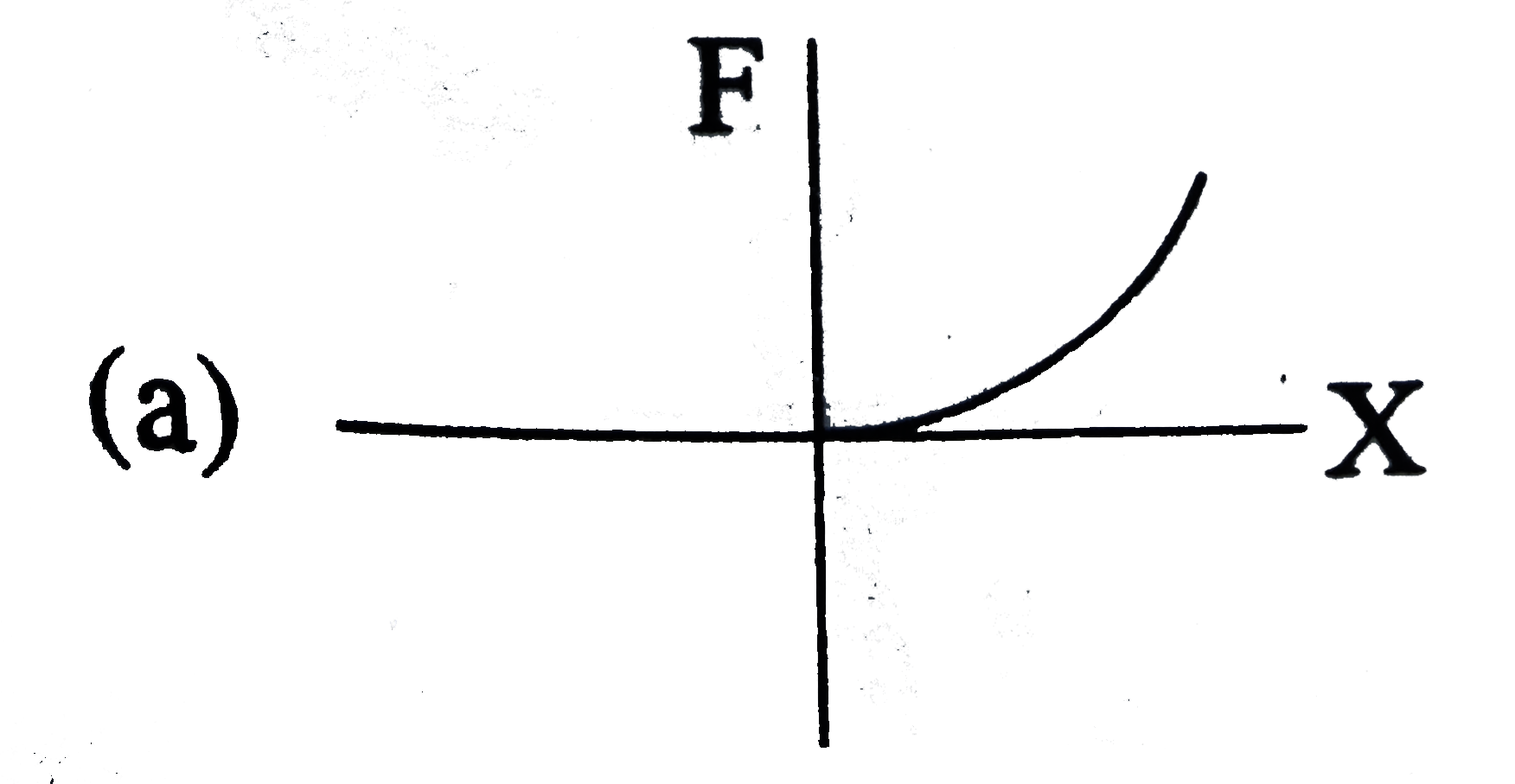 B
B C
C D
D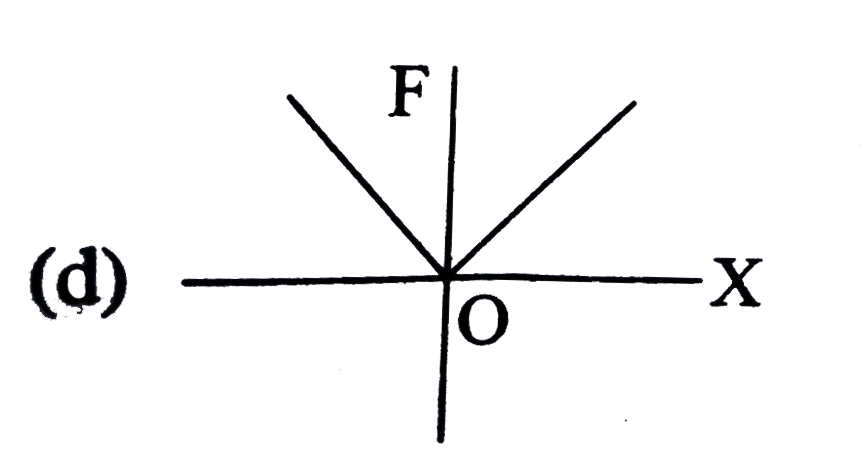
The potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8cm, the potential energy stored in it is
A4UB8UC16UDU4The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is :
A4UB8UC16UDU4
A small trolley of mass 2.0kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation a speed of 600rpm, the length of stretched spring is 50cm. If the original length of the spring is 42cm, find the force constant of the spring.
View SolutionThe potential energy of a spring, when stretched through a distance x is 50J. What would be the work done in stretching it further through the same distance?
View SolutionA mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is 2.0×102 N/m. Calculate the displacement x.
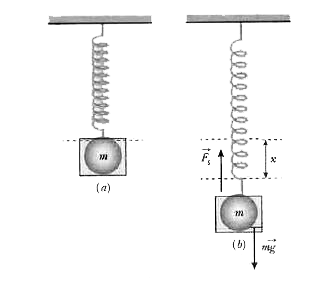
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
View SolutionIf the potential energy of a spring is V on stretching it by 2cm, then its potential energy when it is stretched by 10cm will be
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View Solution