Question

A body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity $(s/v)$ varies with time $t$ as

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem step by step, we need to analyze the relationship between displacement (s), velocity (v), and time (t) when a body is moved from rest by a machine delivering constant power.

Step 1: Understand the relationship between power, work, and time
Given that the power (P) is constant, we can express the work done (W) as:
\( W = P \cdot t \)
where \( t \) is the time.

Step 2: Relate work done to kinetic energy
The work done on the body is equal to the change in kinetic energy (KE). Since the body starts from rest, the kinetic energy can be expressed as:
\( KE = \frac{1}{2} m v^2 \)
Thus, we have:
\( P \cdot t = \frac{1}{2} m v^2 \)

Step 3: Solve for velocity (v)
Rearranging the equation gives us:
\( v^2 = \frac{2Pt}{m} \)
Taking the square root, we find:
\( v = \sqrt{\frac{2Pt}{m}} \)

Step 4: Relate displacement (s) and velocity (v)
Since velocity is defined as the rate of change of displacement with respect to time, we can write:
\( v = \frac{ds}{dt} \)
Substituting our expression for \( v \) gives:
\( \frac{ds}{dt} = \sqrt{\frac{2Pt}{m}} \)

Step 5: Separate variables and integrate
We can rearrange this to separate variables:
\( ds = \sqrt{\frac{2P}{m}} \cdot t^{1/2} dt \)
Now we will integrate both sides. The left side integrates from 0 to \( s \) and the right side from 0 to \( t \):
\( \int ds = \sqrt{\frac{2P}{m}} \int t^{1/2} dt \)

Step 6: Perform the integration
The integral of \( t^{1/2} \) is:
\( \int t^{1/2} dt = \frac{2}{3} t^{3/2} \)
Thus, we have:
\( s = \sqrt{\frac{2P}{m}} \cdot \frac{2}{3} t^{3/2} \)

Step 7: Find the ratio \( \frac{s}{v} \)
Now, we need to find the ratio \( \frac{s}{v} \):
Using our expressions for \( s \) and \( v \):
\( \frac{s}{v} = \frac{s}{\sqrt{\frac{2Pt}{m}}} \)
Substituting for \( s \):
\( \frac{s}{v} = \frac{\sqrt{\frac{2P}{m}} \cdot \frac{2}{3} t^{3/2}}{\sqrt{\frac{2Pt}{m}}} \)

Step 8: Simplify the ratio
This simplifies to:
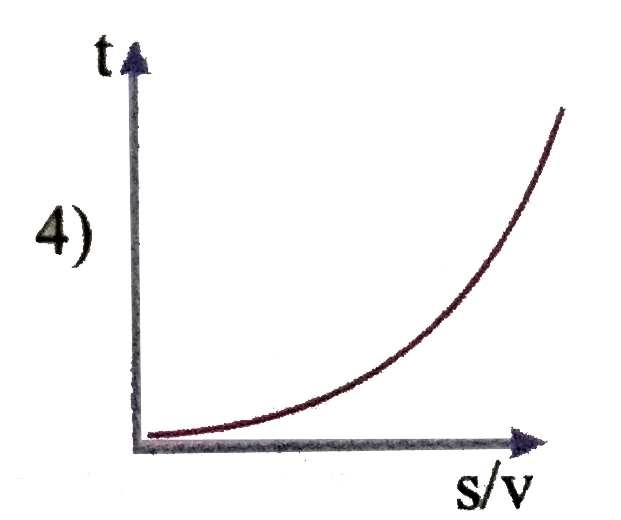
\( \frac{s}{v} = \frac{2}{3} t \)
This shows that the ratio of displacement to velocity varies linearly with time.

Conclusion
Thus, the final answer is:
\( \frac{s}{v} = \frac{2}{3} t \)