A ball is thrown at an angle of incidence 'θ' on a horizontal plane such that the incident direction and the reflected direction are at right angle to each other. If the coefficient of restuitution is 'e' then 'θ' is equal to
tan−1(e)
tan−1(2e)
tan−1(√2e)
tan−1(√e)
The correct Answer is:D
To solve the problem, we need to analyze the motion of the ball when it is thrown at an angle θ and reflects off a horizontal plane. Given that the angle of incidence and the angle of reflection are at right angles to each other, we can derive the relationship involving the coefficient of restitution e.
1. Understanding the Angles:
- Let the angle of incidence be θ.
- The angle of reflection will therefore be 90°−θ because they are complementary (sum to 90 degrees).
2. Velocity Components:
- When the ball is thrown with an initial velocity u, we can resolve this velocity into two components:
- Horizontal component (along the plane): \( u \cos \theta \)
- Vertical component (perpendicular to the plane): \( u \sin \theta \)
3. Velocity After Reflection:
- After the collision with the plane, the vertical component of the velocity will change due to the coefficient of restitution e. The new vertical component of the velocity after reflection will be:
- \( v = e \cdot (u \cos \theta) \)
- The horizontal component remains unchanged:
- \( u \sin \theta \)
4. Using the Right Angle Condition:
- According to the problem, the incident direction and the reflected direction are at right angles to each other. Therefore, we can set up the following relationship using the tangent function:
\(
\tan(90° - \theta) = \frac{u \sin \theta}{e \cdot (u \cos \theta)}
\)
- Simplifying this gives:
\(
\cot(\theta) = \frac{u \sin \theta}{e \cdot (u \cos \theta)}
\)
- This simplifies further to:
\(
\cot(\theta) = \frac{\sin \theta}{e \cos \theta}
\)
5. Rearranging the Equation:
- We can rewrite the cotangent in terms of tangent:
\(
\frac{1}{\tan(\theta)} = \frac{\sin \theta}{e \cos \theta}
\)
- Cross-multiplying gives:
\(
e \sin \theta = \cos \theta \tan(\theta)
\)
6. Final Equation:
- Rearranging leads to:
\(
e = \tan(\theta) \cdot \cot(\theta)
\)
- Since \( \tan(\theta) = \frac{\sin \theta}{\cos \theta} \), we can find that:
\(
e = \frac{\sin^2 \theta}{\cos^2 \theta}
\)
- Thus, we can conclude that:
\(
e = \tan^2(\theta)
\)
7. Finding θ:
- From the equation \( e = \tan^2(\theta) \), we can find θ:
\(
\theta = \tan^{-1}(\sqrt{e})
\)
Conclusion:
The angle θ is given by:
\(
\theta = \tan^{-1}(\sqrt{e})
\)
- Let the angle of incidence be θ.
- The angle of reflection will therefore be 90°−θ because they are complementary (sum to 90 degrees).
- When the ball is thrown with an initial velocity u, we can resolve this velocity into two components:
- Horizontal component (along the plane): \( u \cos \theta \)
- Vertical component (perpendicular to the plane): \( u \sin \theta \)
- After the collision with the plane, the vertical component of the velocity will change due to the coefficient of restitution e. The new vertical component of the velocity after reflection will be:
- \( v = e \cdot (u \cos \theta) \)
- The horizontal component remains unchanged:
- \( u \sin \theta \)
- According to the problem, the incident direction and the reflected direction are at right angles to each other. Therefore, we can set up the following relationship using the tangent function:
\(
\tan(90° - \theta) = \frac{u \sin \theta}{e \cdot (u \cos \theta)}
\)
- Simplifying this gives:
\(
\cot(\theta) = \frac{u \sin \theta}{e \cdot (u \cos \theta)}
\)
- This simplifies further to:
\(
\cot(\theta) = \frac{\sin \theta}{e \cos \theta}
\)
- We can rewrite the cotangent in terms of tangent:
\(
\frac{1}{\tan(\theta)} = \frac{\sin \theta}{e \cos \theta}
\)
- Cross-multiplying gives:
\(
e \sin \theta = \cos \theta \tan(\theta)
\)
- Rearranging leads to:
\(
e = \tan(\theta) \cdot \cot(\theta)
\)
- Since \( \tan(\theta) = \frac{\sin \theta}{\cos \theta} \), we can find that:
\(
e = \frac{\sin^2 \theta}{\cos^2 \theta}
\)
- Thus, we can conclude that:
\(
e = \tan^2(\theta)
\)
- From the equation \( e = \tan^2(\theta) \), we can find θ:
\(
\theta = \tan^{-1}(\sqrt{e})
\)
The angle θ is given by:
\(
\theta = \tan^{-1}(\sqrt{e})
\)
Topper's Solved these Questions
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - NCERT (Based Questions)
45 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Single Answer)
24 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level- II (C.W)
68 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
Show that when a ray of light is incident on the surface of a transparent medium at the polarizing angle, the reflected ray and the refracted ray are at right angles to each other.
View SolutionA ball is thrown with speed u at an angle θ with horizontally. After how much time it will move perpendicular to the initial direction of motion.
View Solution
Knowledge Check
A ball is thrown at an angle θ with the horizontal and the range is maximum. The value of tanθ is:-
A1B√3C1√3D2If a ray of light in a denser medium strikes a rarer medium at an angle of incidence i, the angles of reflection and refraction are respectively, r and r' If the reflected and refraction rays are at right angles to each other, the critical angle for the given pair of media is
Asin−1(tanr')Bsin−1(tanr)Ctan−1(sini)Dcot−1(tani)A ray of light is incident at an angle of 35∘ on a plane mirror. What is the angle between the incident and the reflected rays ?
A90∘B100∘C110∘Dnone of these
A mirror is inclined at an angle of θ with the horizontal. If a ray of light is incident at an angle of incidence θ then the reflected ray makes the following angle with the horizontal
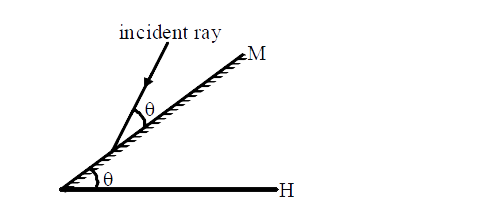
View SolutionUnpolarized light is incident on a plane glass surface. The angle of incidence so that reflected and refracted rays and perpendicular to each other, then
View SolutionA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :

View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray of light is incident at an angle in incidence θ then the reflected ray will make the angle with horizontal, is
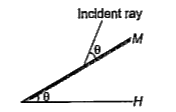
View SolutionAngle of incidence is equal to the angle of reflection.
View Solution
