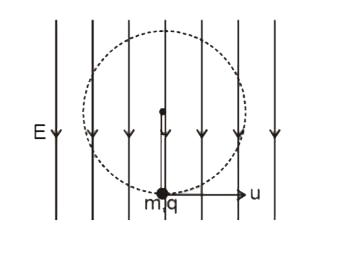
A particle of mass $M$ attached to an inextensible strintg is moving in a vertical circle of radius $R$ .about fixed point $O$ . It is imparted a velocity $u$ in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height $h$ can be calculated by using formula $v^{2} = u^{2} - 2 g h$
(ii) Particle will complete the circle if $u \geq \sqrt{5 g R}$
(iii) Particle will oscillates in lower half $(0^{\circ} < θ \leq 90^{\circ})$ if $0 < u \leq \sqrt{2 g R}$
(iv) The magnitude of tension at a height $' h'$ is calculated by using formula $T = \frac{M}{R} [u^{2} + [g R - 3 g h]]$

If $M = 2 k g, R = 2 m$ and $u = 10 m / s$ . Then velocity of particle when $θ = 60^{\circ}$ is

$2 \sqrt{5} m / s$

$4 \sqrt{5} m / s$

$5 \sqrt{2} m / s$

$5 m / s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

At $θ = 60^{\circ} h = R - R cos 60 = \frac{R}{2}$
Put $h = \frac{R}{2}$ i n $v^{2} - u^{2} = 2 g h$ .

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A particle of mass $M$ attached to an inextensible strintg is moving in a vertical circle of radius $R$ .about fixed point $O$ . It is imparted a velocity $u$ in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height $h$ can be calculated by using formula $v^{2} = u^{2} - 2 g h$
(ii) Particle will complete the circle if $u \geq \sqrt{5 g R}$
(iii) Particle will oscillates in lower half $(0^{\circ} < θ \leq 90^{\circ})$ if $0 < u \leq \sqrt{2 g R}$
(iv) The magnitude of tension at a height $' h'$ is calculated by using formula $T = \frac{M}{R} [u^{2} + [g R - 3 g h]]$

If $R = 2 m, M = 2 k g$ and $u = 12 m / s$ . Then value of tension at lowest position is
A $120 N$
B $164 N$
C $264 N$
Dzero
Question 2 - Select One
A particle of mass $M$ attached to an inextensible strintg is moving in a vertical circle of radius $R$ .about fixed point $O$ . It is imparted a velocity $u$ in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height $h$ can be calculated by using formula $v^{2} = u^{2} - 2 g h$
(ii) Particle will complete the circle if $u \geq \sqrt{5 g R}$
(iii) Particle will oscillates in lower half $(0^{\circ} < θ \leq 90^{\circ})$ if $0 < u \leq \sqrt{2 g R}$
(iv) The magnitude of tension at a height $' h'$ is calculated by using formula $T = \frac{M}{R} [u^{2} + [g R - 3 g h]]$

Tension at highest point of its trajectory in above question will be
A $100 N$
B $44 N$
C $144 N$
D $264 N$
Question 3 - Select One
A particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is $v_{0}$ to complete the vertical circle. The tension in the string when it becomes horizontal is
A $\frac{3 m v_{0}^{2}}{r}$
B $\frac{9 m v_{0}^{2}}{r}$
C3mg
Dboth (A) and (C) are correct