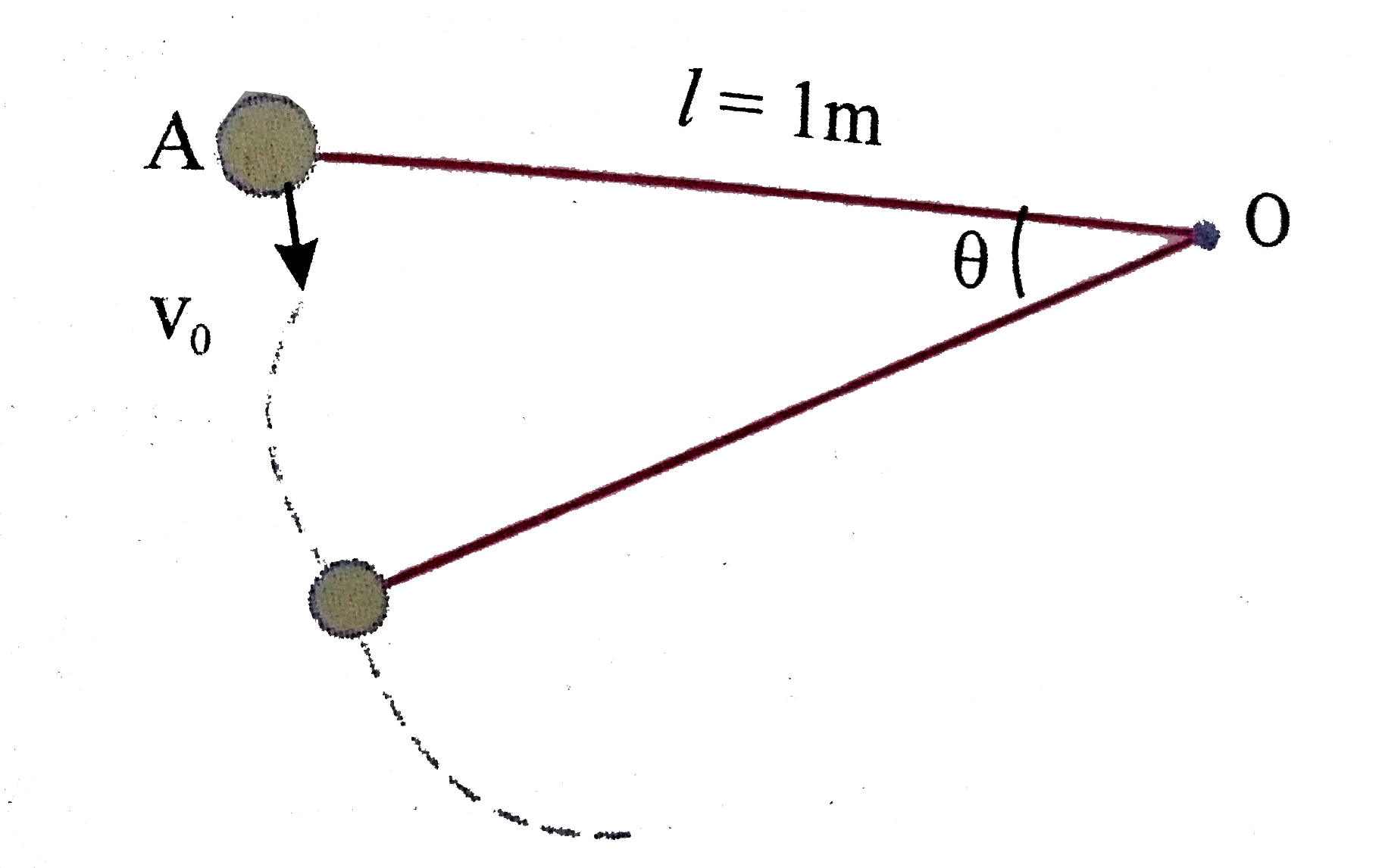
The sphere at P is given a down ward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal, knowing that it can withstand a maximum tension equal to four times the weight of the sphere. then the value of v0 will be (g=10m/s2).
 .
.
The correct Answer is:5
T−mgsinθ=mv2R ltbtgt 4mg−mgsin30=m(v20+2glsin30)l
v0=√5g2.
Topper's Solved these Questions
Similar Questions
The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
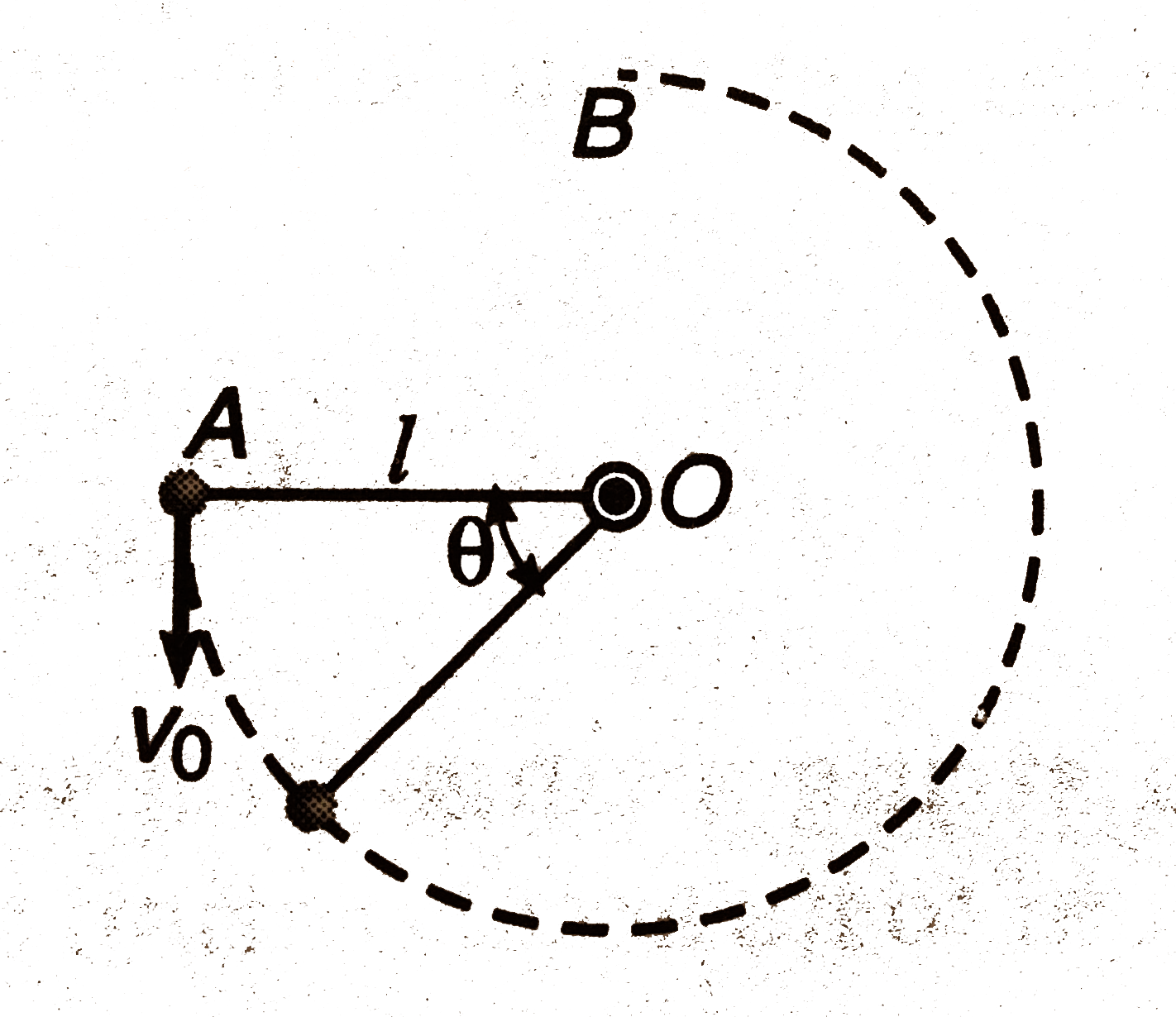
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View Solution
Knowledge Check
The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
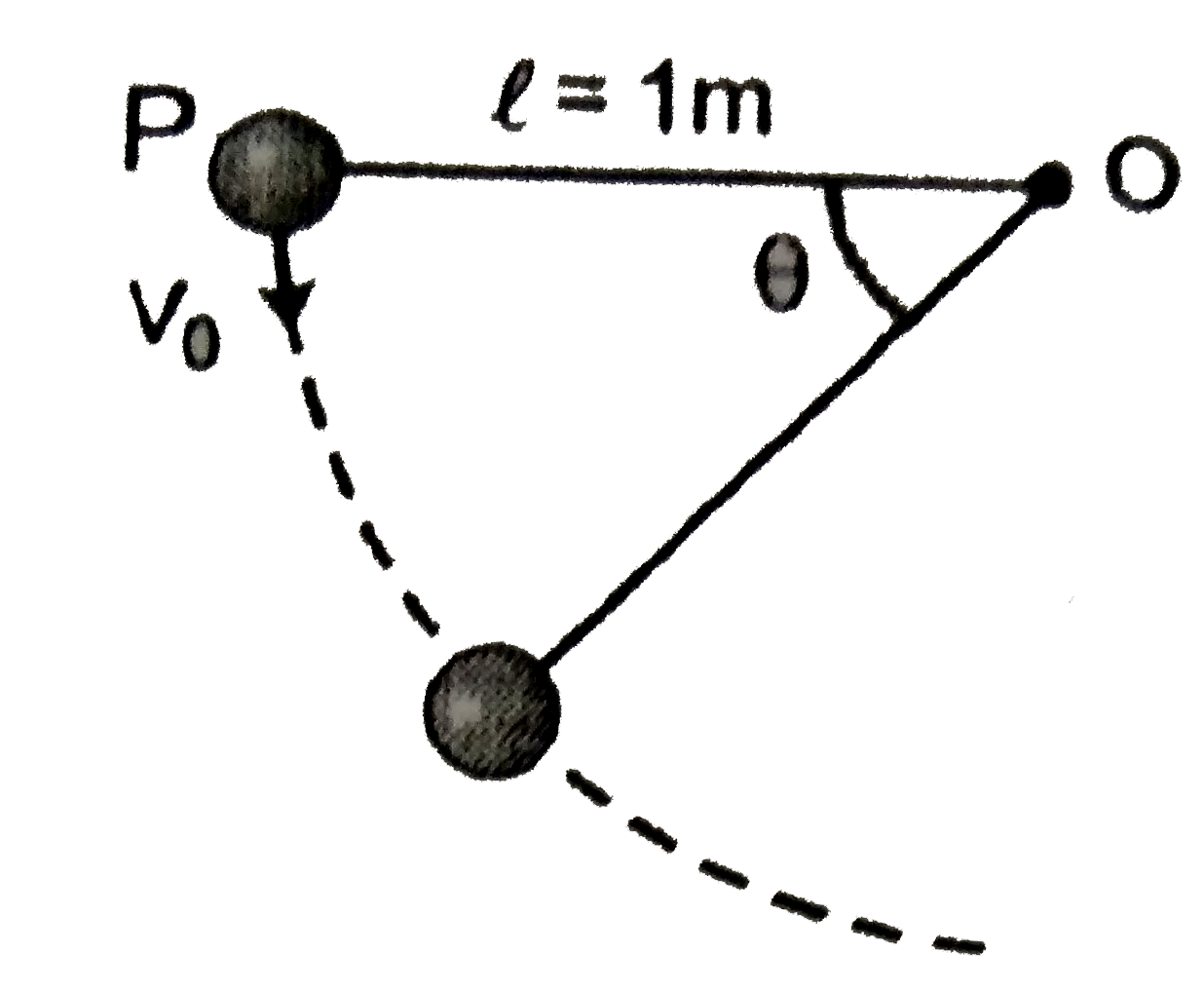 Ag2m/sB2g3m/sC√3g2m/sDwill have minimum value 38m
Ag2m/sB2g3m/sC√3g2m/sDwill have minimum value 38mA small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
 A(a) cos−123B(b) cos−1(14)C(c) 60∘D(d) 30∘
A(a) cos−123B(b) cos−1(14)C(c) 60∘D(d) 30∘A monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is:
(g=10m/s2)A2m/s2B3m/s2C4m/s2D5m/s2
Tension in the rope at the rigid support is (g=10m/s2)
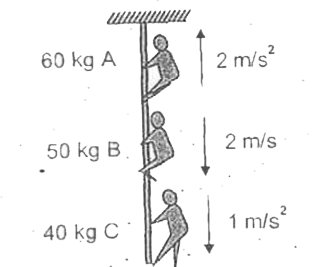
View SolutionTwo persons are holding a rope of negligible mass horizontally. A 20 kg mass is attached to the rope at the midpoint, as a result the rope deviates from the horizontal direction. The tension required to completely straighten the rope is (g=10m/s2)
View SolutionA body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m/s2
View SolutionA monkey of mass 40 kg climbs on a massless rope which can stand a maximum tension of 500 N. In which of the following cases will the rope break? (Take g=10ms−2)

View SolutionA rope of mass 5 kg is hanging between two supports as shown. The tension at the lowest point of the rope is close to (take g = 10m/s2)

View Solution
