The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
V=K√s
dSdt=K√S⇒∫S0dS√S=∫t0Kdt
⇒2√S=KtandS=14K2t2
⇒V=dSdt=14K22t=12K2t
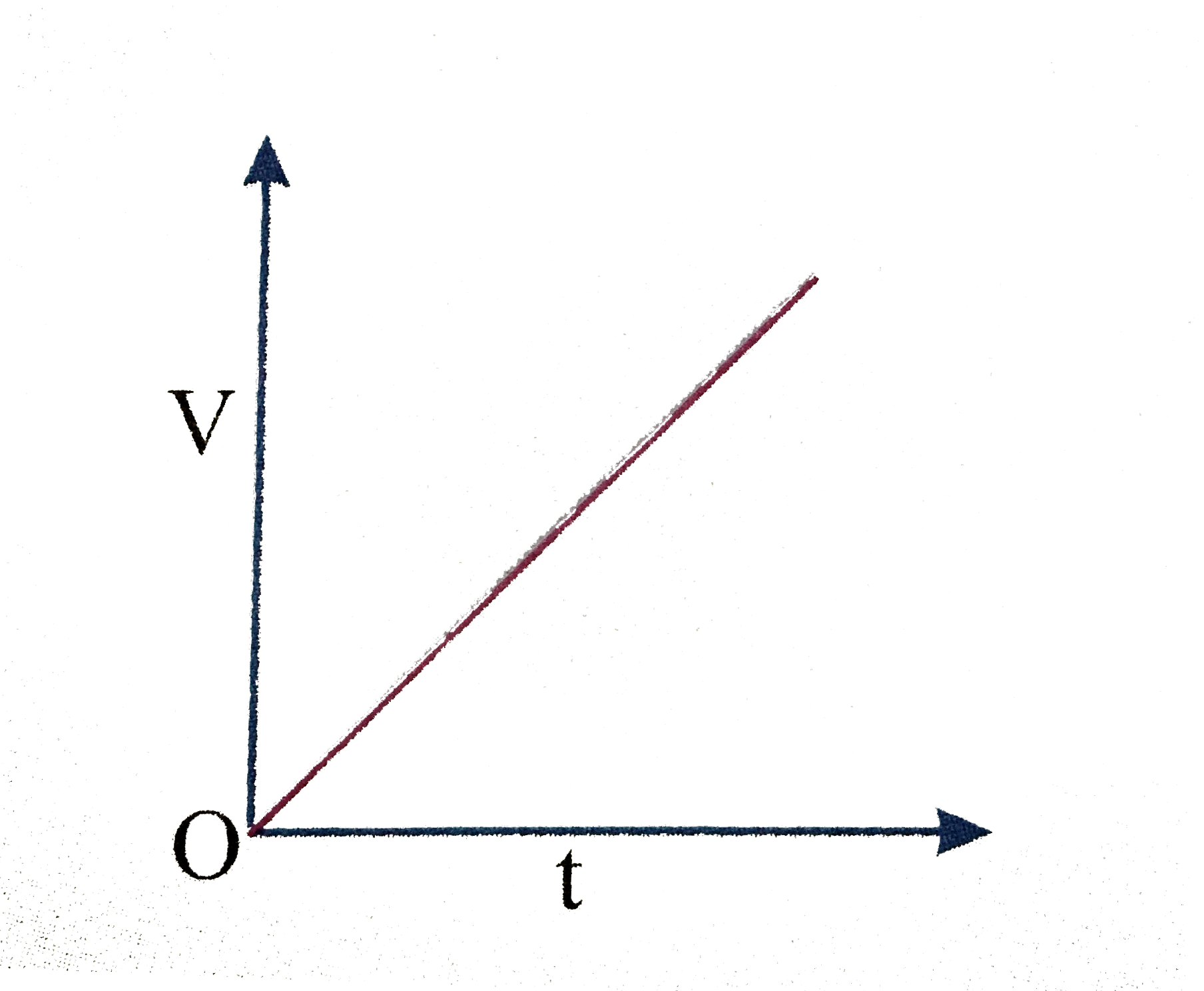
⇒V∝t
∴V∝t
∴ The V-t graph is a straight line passing through the origin.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - C.U.Q42videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 1 C.W20videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
Similar Questions
The velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.View Solution
Knowledge Check
- Question 1 - Select One
The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
A12.5ms−2B7.5ms−2C5ms−2D2.5ms−2 - Question 2 - Select One or More
The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
AThe initial velocity of the particle is zeroBthe initial velocity of the particle is 2.5ms.CThe accelration of the particle is 2.5ms2.DThe acceleration of the particle is 50ms2. - Question 3 - Select One
A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
AThe maximum displacement of the particle from the starting point is u√bBThe particle will oscillate about the originCVelocity is maximum at the originDGiven data is insufficient to determine the exact motion of the particle.
The velocity of a particle moving in the positive direction of x-axis varies as v=α√x where α is positive constant. Assuming that at the moment t=0, the particle was located at x=0, find (i) the time dependance of the velocity and the acceleration of the particle and (ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path.
View SolutionThe linear speed of a particle moving in a circle of radius R varies with time as v=v0−kt, where k is a positive constant. At what time the magnitudes of angular velocity and angular acceleration will be equal ?
View SolutionThe speed (v) of a particle moving in a circle of radius R varies with distance s as v=ks where k is a positive constant.Calculate the total acceleration of the particle
View SolutionThe dispkacement of particle is zero at t=0 and it is x , at t−t. It starts moving in the positive x-direction with a velocity which varices as v=k√x, where (k) is a constant. Show that velocity is directly proprtional to time.
View SolutionThe displacement to particle is zero at t=0andiszatt=t. It starts moving in the positive x-direction with a velocity which varies, v=k√x, wher (k) is a constant. Find the relation for variation of velocity with time.
View Solution

