If a body travles 30 m in an interval of 2 s and 50 m in the next interval of 2s. Then the acceleration of the body is
10m/s2
5m/s2
20m/s2
25m/s2
The correct Answer is:B
To solve the problem step by step, we will use the equations of motion under constant acceleration.
1. Understanding the Problem:
- The body travels 30 m in the first 2 seconds.
- It travels 50 m in the next 2 seconds (total time = 4 seconds).
2. Using the Equation of Motion:
- The equation of motion we will use is:
S=ut+12at2
- Where:
- S = distance traveled
- u = initial velocity
- a = acceleration
- t = time
3. Setting Up the First Equation:
- For the first interval (0 to 2 seconds):
S1=30m,t1=2s
30=u⋅2+12a⋅(22)
30=2u+2a
Dividing the whole equation by 2:
15=u+a(Equation 1)
4. Setting Up the Second Equation:
- For the second interval (2 to 4 seconds):
- Total distance traveled in 4 seconds is:
S2=30+50=80m,t2=4s
80=u⋅4+12a⋅(42)
80=4u+8a
Dividing the whole equation by 4:
20=u+2a(Equation 2)
5. Solving the Equations:
- Now we have two equations:
- Equation 1: 15=u+a
- Equation 2: 20=u+2a
- We can subtract Equation 1 from Equation 2:
(20−15)=(u+2a)−(u+a)
5=a
6. Conclusion:
- The acceleration a of the body is 5m/s2.
- The body travels 30 m in the first 2 seconds.
- It travels 50 m in the next 2 seconds (total time = 4 seconds).
- The equation of motion we will use is:
S=ut+12at2
- Where:
- S = distance traveled
- u = initial velocity
- a = acceleration
- t = time
- For the first interval (0 to 2 seconds):
S1=30m,t1=2s
30=u⋅2+12a⋅(22)
30=2u+2a
Dividing the whole equation by 2:
15=u+a(Equation 1)
- For the second interval (2 to 4 seconds):
- Total distance traveled in 4 seconds is:
S2=30+50=80m,t2=4s
80=u⋅4+12a⋅(42)
80=4u+8a
Dividing the whole equation by 4:
20=u+2a(Equation 2)
- Now we have two equations:
- Equation 1: 15=u+a
- Equation 2: 20=u+2a
- We can subtract Equation 1 from Equation 2:
(20−15)=(u+2a)−(u+a)
5=a
- The acceleration a of the body is 5m/s2.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 C.W25videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 3 C.W25videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - C.U.Q42videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
Similar Questions
If the velocity of a body related to displacement x is given by v=√5000+24x m/s, then the acceleration of the body is _______m/s2.
View Solution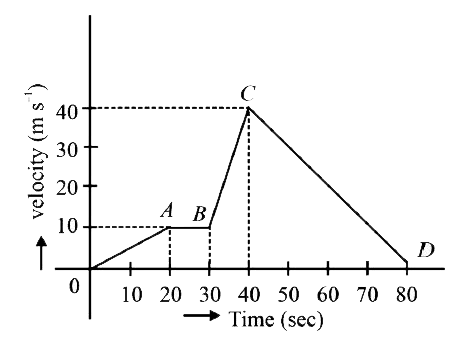
From the above velocity-time graph of a body, identify the interval of time in which the acceleration is maximum. The distance travelled by the body in this interval be Xm. Then what is x10 ?View Solution
Knowledge Check
- Question 1 - Select One
A body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
Aa+bt2Bb−at2C2b−a2t2Db−2at2 - Question 2 - Select One or More
Due to an acceleration of 2 m/s2 the velocity of a body increases from 20 m/s to 30 m/s in a certain period. Find the displacement (in m) of the body in that period.
A650B125C250D325 - Question 3 - Select One
If a body moving with an initial velocity of 3 m/s and an acceleration of 2m/s2. Then what will be the distance travelled by the body in 4th second.
A6 mB7 mC10 mD28 m
Due to an acceleration of 1 m/s2 the velocity of a body increases from 15 m/s to 20 m/s in a certain period. Find the displacement (in m) of the body in that period.
View SolutionDue to an acceleration of 4 m/s2 the velocity of a body increases from 10 m/s to 30 m/s in a certain period. Find the displacement (in m) of the body in that period.
View SolutionA body is moving with a uniform acceleration coverss 40m in the first 4 s and 120m in next 4s. Its initial velocity and acceleration are
View SolutionA body travels uniformly a distance of (10.2±0.4) m in a time interval (6.0±0.2)s. The speed of the particle is best expressed as (in m/s−1).
View SolutionDue to an acceleration of 1 m/s2 the velocity of a body increases from 5 m/s to 10 m/s in a certain period. Find the displacement (in m) of the body in that period.
View Solution

