For the one dimensional motion, described by
for all
for all
for all
lies between 0 and 2
The correct Answer is:A, D
velocity
Acceleration
As acceleration for all
Hence, for all
velocity
When velocity
Hence, v lies between 0 and 2.
Acceleration
When
When
When
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Passage Type Questions
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Multiple Answer Question
22 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Single Type Question
23 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
Similar Questions
The motion of a particle executing SHM in one dimension is described by x=−0.5sin(2t+π/4) where x is in meters and t in seconds. The frequency of oscillation in Hz is
View SolutionFigure gives the x-t plot of a particle is one dimensional motion. Give the signs of position, velocity and acceleration of the particle at t = 0.3s

View Solution
Knowledge Check
Force on a particle in one-dimensional motion is given by F=Av+Bt+CxAt+D, where F= force, v= speed, t= time, x= position and A, B, C and D are constants. Dimension of C will be-
AM2L−2T0BML−1T0CM2L0T−2DNone of theseIn the one-dimensional motion of a particle, the relation between position x and time t is given by x2+2x=t (here x>0). Choose the correct statement.
AThe retardation of the particle is 14(x+1)3BThe uniform velocity of the particle is 1(x+1)3CBoth are correctDBoth are wrongIn one dimensional motion, instantaneous speed y satisfies the condition 0 −VoT<x<voT
3) the acceleration is always a 1 - negative number 4) the motion has no turning pointsAthe displacement in time T must always take non- negative valuesBthe displacement in time T satistics : −v0T<x<v0TCthe acceleration is always a non - negative numberDthe motion has no turning points
Which of the following graphs cannot represent one dimensional motion of a particle?
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval t1 to t2?
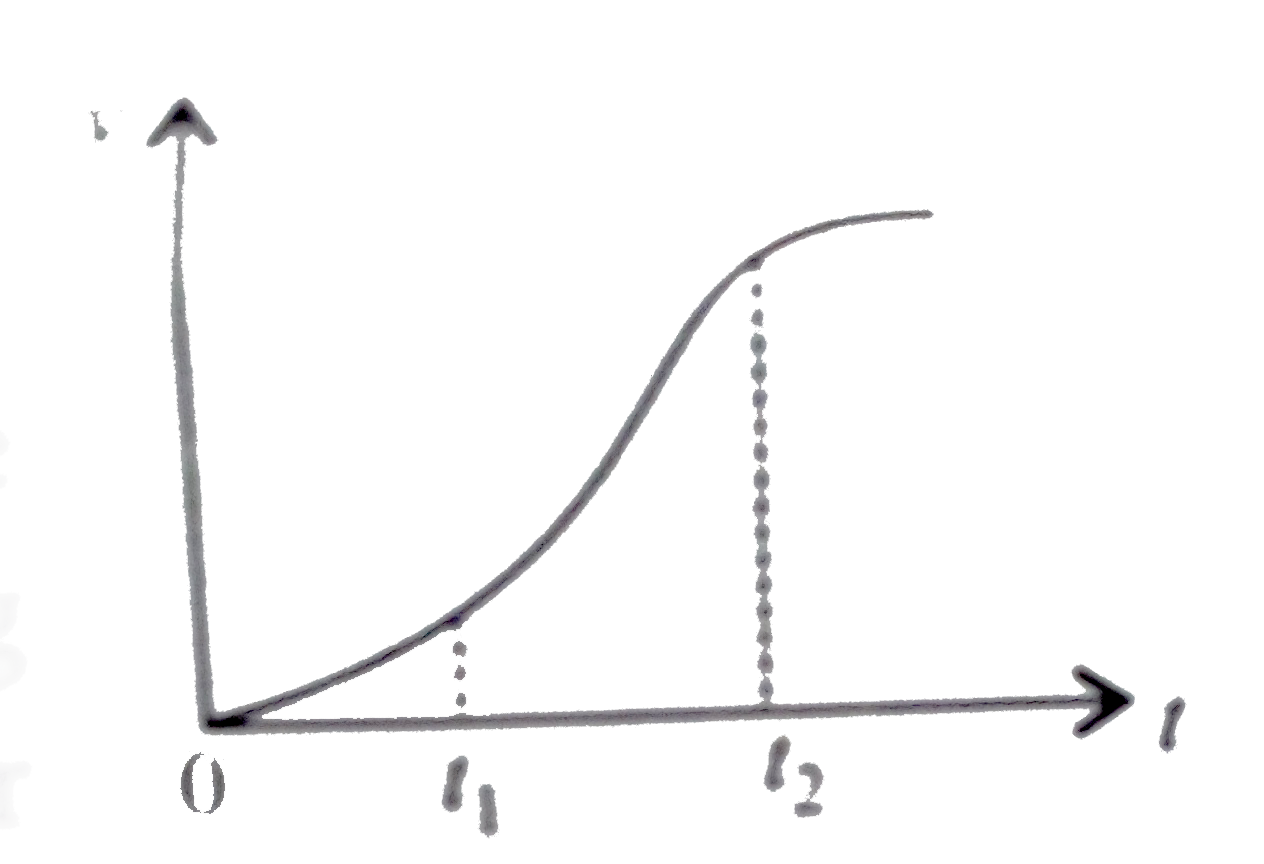
View SolutionDuring one dimensional motion on x-axis Velocity time graph for particle is given.
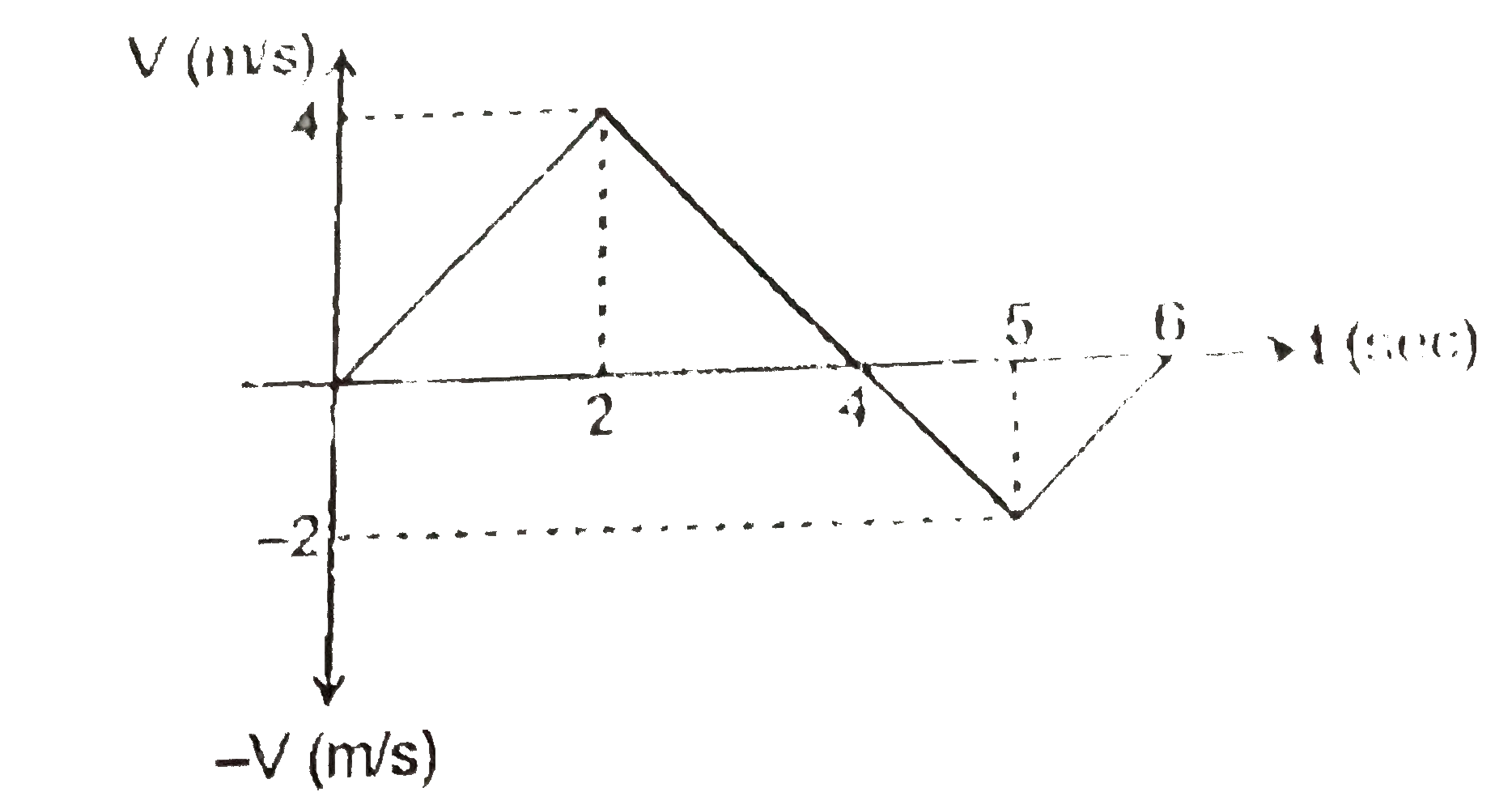
Average acceleration between (t = 0 sec) to (t = 6 sec)
View SolutionA body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
View SolutionA body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
View Solution
