A train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the speed of the train when the passenger catches it for the critical distance:
8m/s
10m/s
12m/s
15m/s
The correct Answer is:B
To solve the problem step-by-step, we will analyze the motion of both the train and the passenger, and find the speed of the train when the passenger catches it at the critical distance.
Step 1: Understand the motion of the train
The train starts from rest with a constant acceleration a=1m/s2. The initial velocity u of the train is 0m/s.
Using the equation of motion:
s=ut+12at2
Since u=0:
s=12at2=12(1)t2=t22
Step 2: Understand the motion of the passenger
The passenger runs at a constant speed of vp=10m/s. The distance covered by the passenger when he catches the train is given by:
dp=vp⋅t=10t
Step 3: Set up the equation for the distances
The passenger starts at a distance S=25.5m behind the train. When the passenger catches the train, the total distance covered by the passenger will be equal to the distance covered by the train plus the initial distance S:
dp=S+dt
Substituting the expressions for dp and dt:
10t=25.5+t22
Step 4: Rearranging the equation
Rearranging the equation gives:
t22−10t+25.5=0
Multiplying through by 2 to eliminate the fraction:
t2−20t+51=0
Step 5: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−20,c=51:
t=20±√(−20)2−4⋅1⋅512⋅1
t=20±√400−2042
t=20±√1962
t=20±142
This gives two solutions:
t=342=17sandt=62=3s
Step 6: Determine the relevant time
The passenger catches the train first at t=3s. The second time t=17s indicates that the passenger will eventually be caught by the train again after running ahead.
Step 7: Calculate the speed of the train when the passenger catches it
Using the formula for final velocity:
v=u+at
Substituting u=0m/s, a=1m/s2, and t=10s (since we are interested in the critical distance):
v=0+1⋅10=10m/s
Final Answer
The speed of the train when the passenger catches it for the critical distance is 10m/s.
---
The train starts from rest with a constant acceleration a=1m/s2. The initial velocity u of the train is 0m/s.
s=ut+12at2
Since u=0:
s=12at2=12(1)t2=t22
The passenger runs at a constant speed of vp=10m/s. The distance covered by the passenger when he catches the train is given by:
dp=vp⋅t=10t
The passenger starts at a distance S=25.5m behind the train. When the passenger catches the train, the total distance covered by the passenger will be equal to the distance covered by the train plus the initial distance S:
dp=S+dt
Substituting the expressions for dp and dt:
10t=25.5+t22
Rearranging the equation gives:
t22−10t+25.5=0
Multiplying through by 2 to eliminate the fraction:
t2−20t+51=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=1,b=−20,c=51:
t=20±√(−20)2−4⋅1⋅512⋅1
t=20±√400−2042
t=20±√1962
t=20±142
This gives two solutions:
t=342=17sandt=62=3s
The passenger catches the train first at t=3s. The second time t=17s indicates that the passenger will eventually be caught by the train again after running ahead.
Using the formula for final velocity:
v=u+at
Substituting u=0m/s, a=1m/s2, and t=10s (since we are interested in the critical distance):
v=0+1⋅10=10m/s
The speed of the train when the passenger catches it for the critical distance is 10m/s.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Multiple Answer Question22videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Integer Type Question13videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than One Option Question7videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
Similar Questions
A train starts from rest and moves with a constant accelerationof 2.0ms2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find a. the total distance moved by the train, b. the maximum speed attained by the train and c. the position(s) of the train at half the maximum speed.
View SolutionA train starts from a station and moves with a constant acceleration for 2 minutes. If it covers a distance of 400m in this period, find the acceleration.
View Solution
Knowledge Check
- Question 1 - Select One
A train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the critical distance Sc for which passenger will take the ten seconds time to catch the trainA50 mB35 mC30 mD25 m - Question 2 - Select One
A train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
If S=25.5 m and passenger keeps running, find the time in which he will catch the train:A5 secB4 secC3 secD2√2 sec - Question 3 - Select One or More
A train starts from rest at S=0 and is subjected to an acceleration as shown in figure. Then,
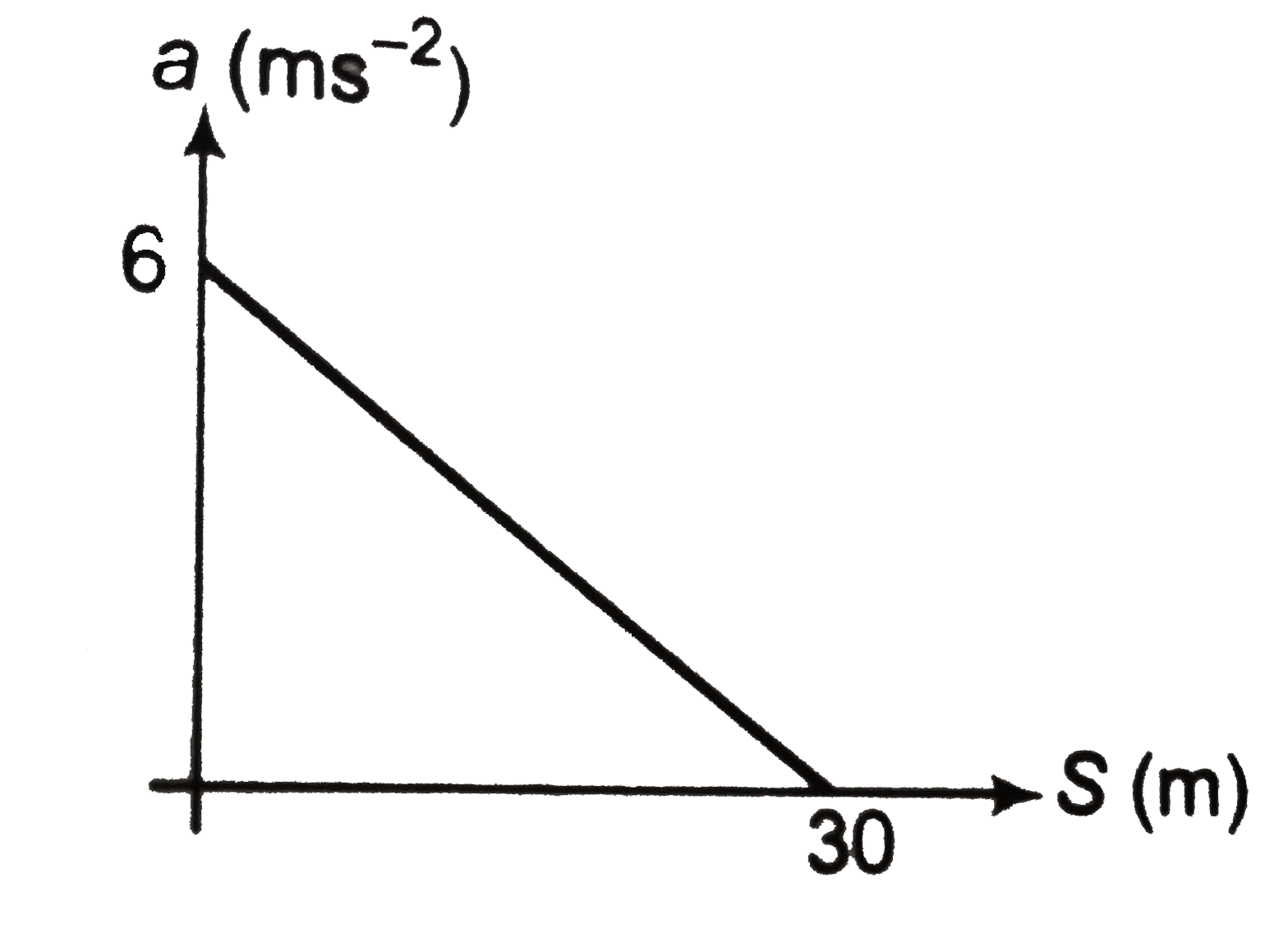 Avelocity at the end of 10 m displacement is 20ms−1Bvelocity of the train at S=10m is 10ms−1CThe maximum velocity attained by train is √180ms−1DThe maximum velocity attained by the train is 15 ms^-1
Avelocity at the end of 10 m displacement is 20ms−1Bvelocity of the train at S=10m is 10ms−1CThe maximum velocity attained by train is √180ms−1DThe maximum velocity attained by the train is 15 ms^-1
A train starting from rest moves with a uniform acceleration of 0.2m/s2 for 5 minutes . Calculate the speed acquired and the distance travelled in this time.
View SolutionWhen did the first passenger train started in India?
View SolutionA train overtakes a person walking at 1 m/s in 5 s.
If the speed of the train is 65 m/s, then what is the length of the train?View SolutionA train overtakes a person walking at 1 m/s in 5 s.
If the speed of the train is 65 m/s, then what is the length of the train?View Solution12. A train of length 200m crosses a platform of length 100m in 12 seconds. Find the speed ofthe train (in m/s)a) 40b) 25d) 18c) 60
View Solution

