Two particles A and B start from rest at the origin $x = 0$ and move along a straight line such that $a_{A} = (6 t - 3) m s^{- 2}$ and $a_{B} = (12 t^{2} - 8) m s^{- 2}$ where t is in seconds based on the above facts answer the following questions,
Total distance travelled by A at $t = 4$ s is

A

40 m

B

41 m

C

42 m

D

43 m

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

For A
$d v_{A} = a_{A} d t \Rightarrow \int_{0}^{v_{A}} d v_{A} = \int_{0}^{t} (6 t - 3) d t \Rightarrow V_{A} = 3 t^{2} - 3 t$
$d v_{B} = a_{B} d t \Rightarrow \int_{0}^{v_{0}} d v_{B} = \int_{0}^{t} (12 t^{2} - B) d t$
$\Rightarrow V_{B} = 4 t^{3} - 8 t$
Let us now calculate the times when A and B are at rest. The particle A is rest $(V_{A} = 0)$ when
$3 t^{2} - 3 t = 0 \Rightarrow t = 0$ and $t = 1$ s
The particle B is at rest $(V_{B} = 0)$ , when $4 t^{3} - 8 t = 0 \Rightarrow t = 0 s$ and $t = \sqrt{2} s$
The position of particles A and B can be determined
using $v = \frac{d x}{d t}$ so ${d x}_{A} = V_{A} d t$
$\Rightarrow \int_{0}^{X_{A}} {d x}_{A} = \int_{0}^{t} (3 t^{2} - 3 t) d t$
$\Rightarrow X_{A} = t^{3} - \frac{3}{2} t^{2}$ similarly $d X_{B} = V_{B} d t$
$\Rightarrow \int_{0}^{X_{B}} {d x}_{B} = \int - {(0)}^{t} (4 t^{3} - 8 t) d t \Rightarrow X_{B} = t^{4} - 4 t^{2}$
The position of particle A at $t = 1$ s and 4 s are
$X_{A} ∣ t = 1 s$ $= 1^{3} - \frac{3}{2} - \frac{3}{2} (1^{2}) = 0.5 m$
$X_{A} ∣ t = 4 s$ $= 4^{3} - \frac{3}{2} (4^{2}) = 40 m$
Particle A has travelled a total distance given by $d_{A} = 2 (0.5) + 40 = 41 m$
The position of particle B at $t = \sqrt{2}$ s and 4 s
are $X_{B} ∣ t = \sqrt{2} = {(\sqrt{2})}^{4} - 4 {(\sqrt{2})}^{2} = - 4 m$
$X_{B} ∣ t = 4 = {(4)}^{4} - 4 {(4)}^{2} = 192 m$
Particle (B) has travelled a total distance given by $d_{B} = 2 (4) + 192 = 200 m$
At $t = 4 s$ s the distance between A and B is
$Δ X_{A B} = 192 - 40 = 152 m$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles A and B start from rest at the origin $x = 0$ and move along a straight line such that $a_{A} = (6 t - 3) m s^{- 2}$ and $a_{B} = (12 t^{2} - 8) m s^{- 2}$ where t is in seconds based on the above facts answer the following questions,
Total distance between them at $t = 4$ s is
A144 m
B148 m
C152 m
D156 m
Question 2 - Select One
Block A and C starts from rest and move to the right with acceleration $a_{A} = 12 t m s^{- 2}$ and $a_{C} = 3 m s^{- 2}$ . Here t is in second. The time when block B again comes to rest is

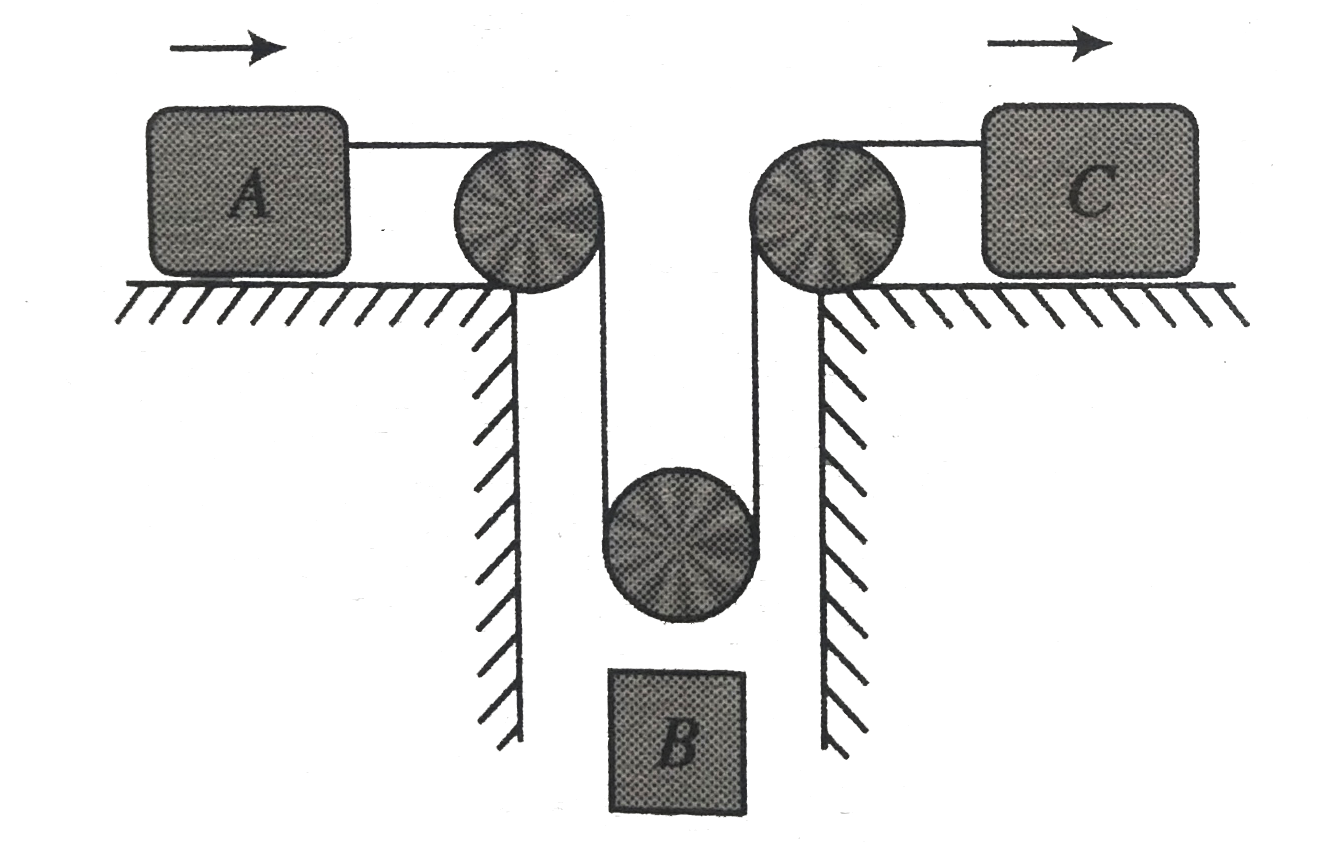A2s
B1s
C $3 / 2 s$
D $1 / 2 s$
Question 3 - Select One
Block A and C start from rest and move to the right with acceleration $a_{A} = 12 t m / s^{2}$ and $a_{C} = 3 m / s^{2}$ Here t is in seconds. The time when block B attain comes to rest is:

A2s
B1s
C $3 / 2 s$
D $1 / 2 s$

NARAYNA-MOTION IN A STRAIGHT LINE-Multiple Answer Question

Home
Ask Doubt
Profile