If ABCD is quadrilateral whose sides represent vectors in cyclic order, →AB is equivalent is
−−→CA+−−→CB
−−→CD
−−→AD+−−→DC+−−→CB
−−→AD+−−→BD
The correct Answer is:C
To solve the problem, we need to determine which vector is equivalent to the vector →AB in the quadrilateral ABCD where the sides represent vectors in cyclic order.
1. Understanding the Quadrilateral:
We have a quadrilateral ABCD with vertices A, B, C, and D. The sides of the quadrilateral represent vectors in a cyclic order: →AB, →BC, →CD, and →DA.
2. Identifying the Vector →AB:
We need to find a vector that is equivalent to →AB. In vector terms, this means we are looking for a vector that has the same magnitude and direction as →AB.
3. Considering the Options:
Let's analyze the options provided to see which vector can be equivalent to →AB:
- Option 1: →CA: This vector points from C to A. It cannot be equivalent to →AB since it points in a different direction.
- Option 2: →CD: This vector points from C to D. Again, it is not equivalent to →AB as it points in a different direction.
- Option 3: →AD: This vector points from A to D. It does not match the direction of →AB.
- Option 4: →AD+→DB: This option combines two vectors. The vector →AD points from A to D and →DB points from D to B. The resultant of these two vectors will indeed point from A to B if we consider the cyclic nature of the quadrilateral.
4. Conclusion:
The only option that correctly represents the vector →AB is the combination of vectors →AD+→DB. Therefore, we conclude that:
→AB=→AD+→DB
Final Answer:
→AB=→AD+→DB
We have a quadrilateral ABCD with vertices A, B, C, and D. The sides of the quadrilateral represent vectors in a cyclic order: →AB, →BC, →CD, and →DA.
We need to find a vector that is equivalent to →AB. In vector terms, this means we are looking for a vector that has the same magnitude and direction as →AB.
Let's analyze the options provided to see which vector can be equivalent to →AB:
- Option 1: →CA: This vector points from C to A. It cannot be equivalent to →AB since it points in a different direction.
- Option 2: →CD: This vector points from C to D. Again, it is not equivalent to →AB as it points in a different direction.
- Option 3: →AD: This vector points from A to D. It does not match the direction of →AB.
- Option 4: →AD+→DB: This option combines two vectors. The vector →AD points from A to D and →DB points from D to B. The resultant of these two vectors will indeed point from A to B if we consider the cyclic nature of the quadrilateral.
The only option that correctly represents the vector →AB is the combination of vectors →AD+→DB. Therefore, we conclude that:
→AB=→AD+→DB
→AB=→AD+→DB
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-III(C.W)48videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. SINGLE ANS.8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-I(C.W)43videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a cyclic quadrilateral, then cosA+cosB is equal to
A0BcosC+cosDC−(cosC+cosD)DcosC−cosD - Question 2 - Select One
ABCD is quadrilateral whose sides touch a given circle. Which of the following is true regarding above statement ?
AAB+AD=CB+CDBAB:CD=AD:BCCAB+CD=AD+BCDAB:AD=CB:CD - Question 3 - Select One
If ABCD is a cyclic quadrilateral then what is sinA+sinB−sinC−sinD equal to ?
A0B1C2D2(sinA+sinB)
In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
 View Solution
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
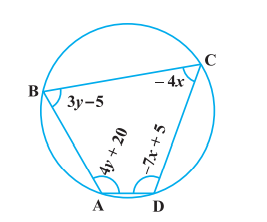 View Solution
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of x
View SolutionABCD is a quadrilateral whose diagnonal AC divides it into two parts, equal in are, then ABCD
View SolutionABCD is a parallelogram whose adjacent sides are represented by he vectors →a and →b. Three of its vertices are A(1,2,3),B(2,0,5) and D(-1,4,1).
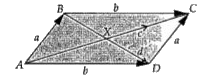
The vector →a= _______.View Solution


