Two particles move in a uniform gravitational field with an acceleration g.At the initial moment the particles were located at same point and moved with velocities u1=9ms−1 and u2=4ms−1 horizontally in opposite directions.The time between the particles at the moment when their velocity vectors are mutually perpendicular in s in (take g=10ms−2)
0.36
3.6
0.6
6
The correct Answer is:C
To solve the problem, we need to determine the time at which the velocity vectors of two particles moving in a gravitational field become mutually perpendicular. Let's break down the solution step by step.
Step 1: Understand the Initial Conditions
Both particles start at the same point and move horizontally in opposite directions with initial velocities:
- Particle 1: u1=9m/s (to the right)
- Particle 2: u2=4m/s (to the left)
Step 2: Determine the Velocity Components
Since both particles are moving under the influence of gravity, their vertical velocity components will change over time while their horizontal components remain constant.
For Particle 1:
- Horizontal velocity: v1x=9m/s
- Vertical velocity: v1y=0−g⋅t=−10tm/s (downward)
For Particle 2:
- Horizontal velocity: v2x=−4m/s (since it moves in the opposite direction)
- Vertical velocity: v2y=0−g⋅t=−10tm/s (downward)
Step 3: Set Up the Condition for Perpendicular Vectors
The velocity vectors of the two particles are mutually perpendicular when their dot product is zero. The dot product of two vectors A=(Ax,Ay) and B=(Bx,By) is given by:
A⋅B=AxBx+AyBy
For our particles:
v1⋅v2=(9)(−4)+(−10t)(−10t)=0
This simplifies to:
−36+100t2=0
Step 4: Solve for Time t
Rearranging the equation gives us:
100t2=36
t2=36100=0.36
Taking the square root:
t=√0.36=0.6s
Step 5: Conclusion
The time at which the velocity vectors of the two particles are mutually perpendicular is t=0.6s.
Summary
- The two particles start at the same point and move horizontally in opposite directions.
- Their vertical velocities change due to gravity.
- The condition for their velocity vectors to be perpendicular leads us to find that t=0.6s.
Both particles start at the same point and move horizontally in opposite directions with initial velocities:
- Particle 1: u1=9m/s (to the right)
- Particle 2: u2=4m/s (to the left)
Since both particles are moving under the influence of gravity, their vertical velocity components will change over time while their horizontal components remain constant.
- Horizontal velocity: v1x=9m/s
- Vertical velocity: v1y=0−g⋅t=−10tm/s (downward)
- Horizontal velocity: v2x=−4m/s (since it moves in the opposite direction)
- Vertical velocity: v2y=0−g⋅t=−10tm/s (downward)
The velocity vectors of the two particles are mutually perpendicular when their dot product is zero. The dot product of two vectors A=(Ax,Ay) and B=(Bx,By) is given by:
A⋅B=AxBx+AyBy
v1⋅v2=(9)(−4)+(−10t)(−10t)=0
This simplifies to:
−36+100t2=0
Rearranging the equation gives us:
100t2=36
t2=36100=0.36
Taking the square root:
t=√0.36=0.6s
The time at which the velocity vectors of the two particles are mutually perpendicular is t=0.6s.
- The two particles start at the same point and move horizontally in opposite directions.
- Their vertical velocities change due to gravity.
- The condition for their velocity vectors to be perpendicular leads us to find that t=0.6s.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-III(C.W)48videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. SINGLE ANS.8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-I(C.W)43videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
Two particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v1=3m/sandv2=4m/s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View Solution
Knowledge Check
- Question 1 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
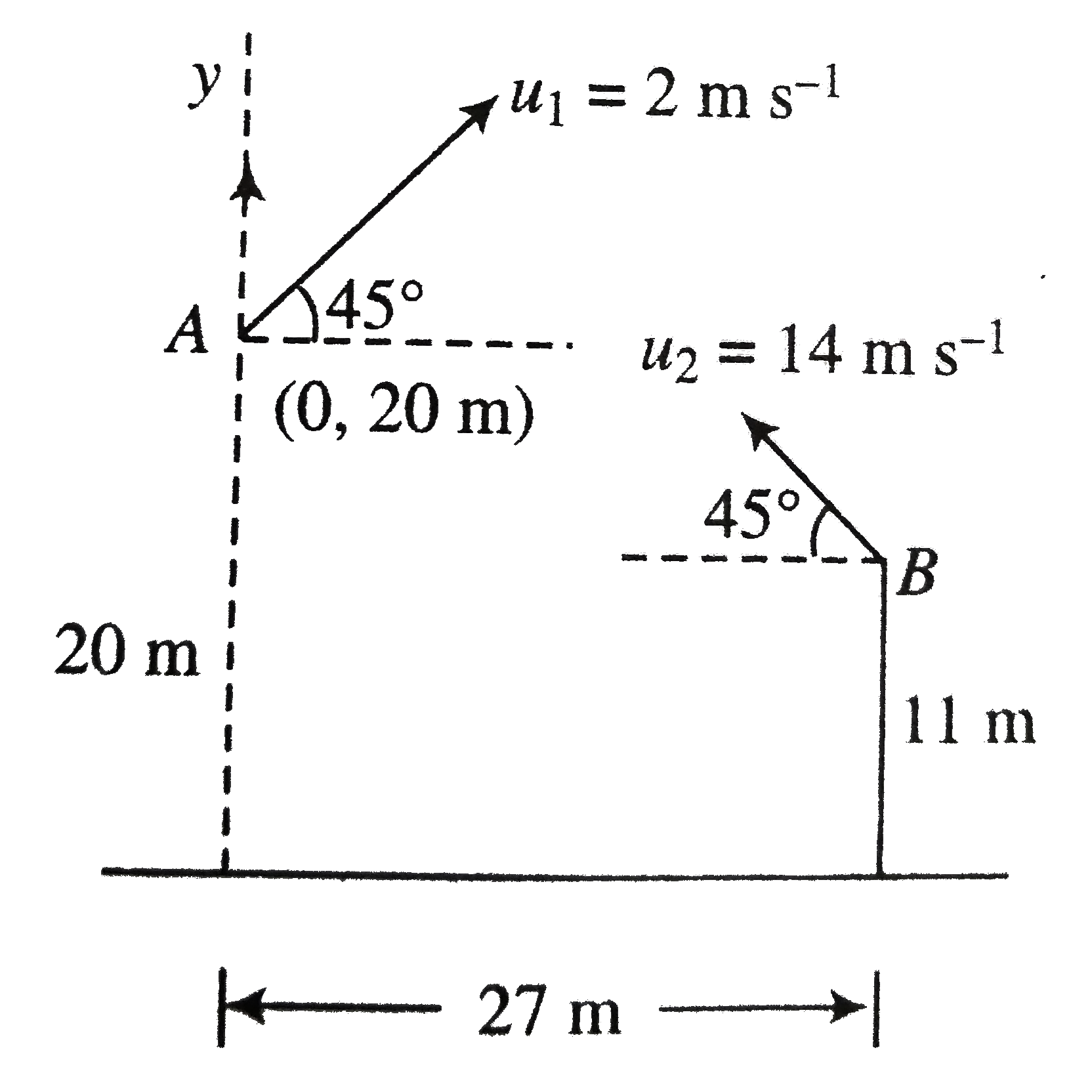
Minimum separation between A and B isA3 mB6 mC12 mD9 m - Question 2 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
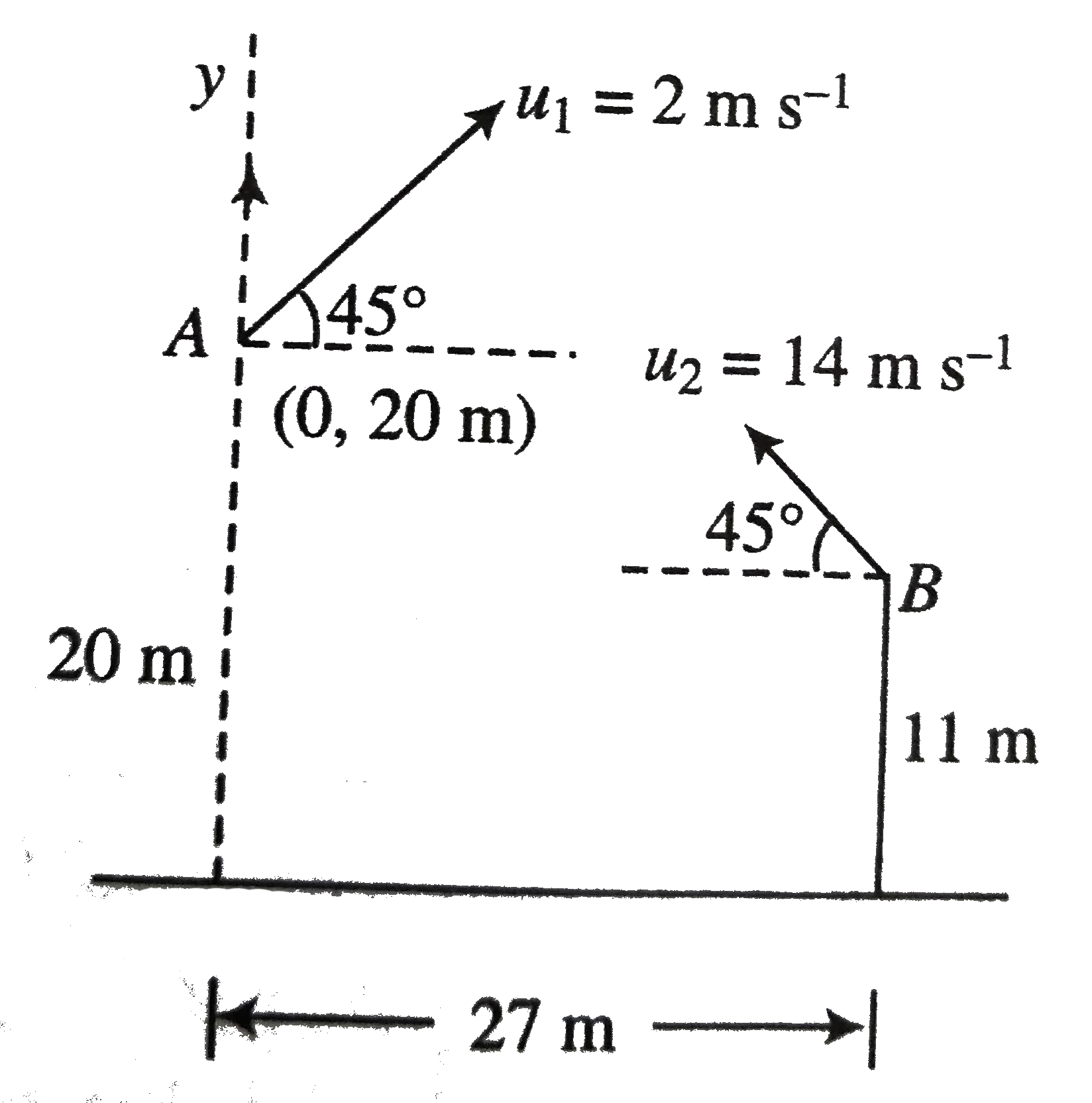
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆj - Question 3 - Select One
A particle is projected with initial velocity of ˆi+2ˆj. The equation of trajectory is (takeg=10ms−2)
Ay=2x−15x2By=2x−25x2Cy=x−5x2Dy=2x−5x2
Two particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionFrom the top of the tower, two balls are thrown horizontally in opposite directions with velocities u1 and u2. Find the distacne between the balls at the moment when their velocity vectors becomes mutually perpendicular. (Assume the height of tower very large)
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
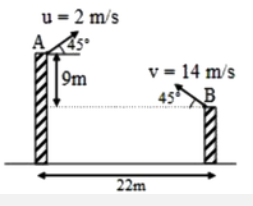 View Solution
View SolutionTwo particles are simultaneously projected in opposite directions horizontally from a given point in space where gravity g is uniform. If u1 and u2 be their initial speeds, then the time t after which their velocitites are mutually perpendicular is given by
View Solution

