Question

Multiplication modulo

Explanation

What is Multiplication modulo?

Let's explore the addition property of modular arithmetic:

(A + B) mod C = (A mod C + B mod C) mod C

Example:

Let A=14, B=17, C=5

Let's verify: (A + B) mod C = (A mod C + B mod C) mod C

LHS = Left Hand Side of the Equation

RHS = Right Hand Side of the Equation

LHS = (A + B) mod C

LHS = (14 + 17) mod 5

LHS = 31 mod 5

LHS = 1

RHS = (A mod C + B mod C) mod C

RHS = (14 mod 5 + 17 mod 5) mod 5

RHS = (4 + 2) mod 5

RHS = 1

LHS = RHS = 1

Intuition Behind Modular Addition

Observe the figure below. If we want to calculate 12+9 mod 7 we can easily go around the modular circle for a sequence of 12+9 steps clockwise (as shown in the bottom left circle).

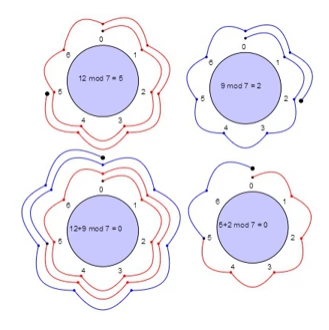
We can take a shortcut by observing that every 7 steps we end up in the same position on the modular circle. These complete loops around the modular circle don’t contribute to our final position. We ignore these complete loops around the circle by calculating each number mod 7 (as shown in the two upper modular circles). This will give us the number of clockwise steps, relative to 0, that contributed to each of their final positions around the modular circle.

Now, we only have to go around the circle clockwise the total of the number of steps that contributed to each of numbers final position (as shown in the bottom right modular circle). This method applies, in general, to any two integers and any modular circle.

Proof for Modular Addition

We will prove that (A + B) mod C = (A mod C + B mod C) mod C

We must show that LHS=RHS

From the quotient remainder theorem we can write A and B as:

A = C * Q1 + R1 where 0 ≤ R1 < C and Q1 is some integer. A mod C = R1

B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2

(A + B) = C * (Q1 + Q2) + R1+R2

LHS = (A + B) mod C

LHS = (C * (Q1 + Q2) + R1+ R2) mod C

We can eliminate the multiples of C when we take the mod C

LHS = (R1 + R2) mod C

RHS = (A mod C + B mod C) mod C

RHS = (R1 + R2) mod C

LHS=RHS= (R1 + R2) mod C

Modular Subtraction

A very similar proof holds for modular subtraction

(A - B) mod C = (A mod C - B mod C) mod C

Let’s have a look at an example

A + B) = C * (Q1 + Q2) + R1+R2

(1）LHS = (A + B) mod C

(2）LHS = (C * (Q1 + Q2) + R1+ R2) mod C

We can eliminate the multiples of C when we take the mod C

LHS = (R1 + R2) mod C



WHAT DOES (3) MEAN BY DETAIL?

Solution

Here's what it means:

If we are calculating X mod C, then:

we can add multiples of C to X or subtract multiples of C from X and the result mod C will not change

i.e. X mod C = (X+ K * C) mod C where K is an integer

e.g. 5 mod 7 = ( 5 + 7 )mod 7 = (5 + 2 * 7) mod 7 = (5 - 29 * 7) mod 7 = (5 + 42 * 7) mod 7 = 5

This is discussed in previous articles

The contribution of the multiple of C mod 7 is 0.

Why is this true?

From the quotient remainder theorem we have:

X = Q * C + R , where 0 <= R < C

Let's add an integer multiple of C to both sides of this equation

i.e. let's add K * C where K is some integer

X + K * C = Q * C + R + K * C

Now we group the terms on the right hand side

X + K * C = (Q + K) * C + R

The result of adding integers Q + K is just another integer

Let's call this new integer G

The result of X + K * C is just another integer

Let's call this new integer Y

Y = G * C + R, where 0 <= R < C

This is the exact form of the quotient remainder theorem!!

Thus the remainder of Y divided by C is R

But Y = X + K * C

So the remainder of X + K * C divided by C is R.

But this means than X and X + K * C have the same remainder R.

So in the specific example

(R1 + R2) mod C = (C * (Q1 + Q2) + R1+ R2) mod C

because this is in the form

X mod C = (X+ K * C) mod C