The area of parallelogram; triangle and quadrilateral in terms of cross product.
Step by step video & image solution for The area of parallelogram; triangle and quadrilateral in terms of cross product. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Which of the following statements are true (T) and which are false (F)? In a parallelogram, the diagonals are equal. In a parallelogram, the diagonals bisect each other. In a parallelogram, the diagonals intersect each other at right angles. In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram. If all the angles of a quadrilateral are equal, it is a parallelogram. If three sides of a quadrilateral are equa, it is a parallelogram. If three angles of a quadrilateral are equal, it is a parallelogram. If all the sides of a quadrilateral are equal it is a parallelogram
View SolutionObtain an expression for the area of a triangle in terms of the cross product of two vectors representing the two sides of the triangle
View SolutionGiven the following statements :
A:If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
B: If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
Identify these as contrapositive or converse of each other.
View SolutionThe area of a parallelogram is equal to the product of a side of the parallelogram and the distance between any two sides.
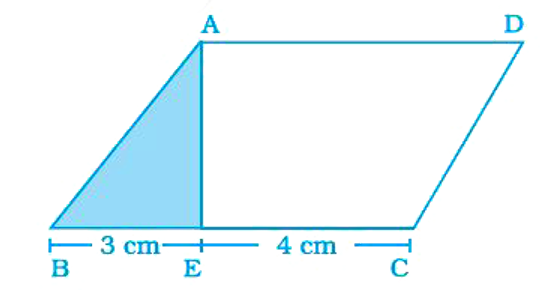
View SolutionIn Fig. 9.35, find the area of parallelogram ABCD if the area of shaded triangle is 9cm2.
View SolutionArea OF Triangle || Quadrilateral || Centres OF Triangle
View SolutionFinding the area of figure which is combinations of triangles and quadrilaterals
View SolutionThe base of a parallelogram is (2x+3) units and the corresponding height is (2x–3) units. Find the area of the parallelogram in terms of x. What will be the area of parallelogram of x=30 units?
View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionStatement -I: A diagonal divides a parallelogram into two triangles of equal areas. Statement - II: Area of parallelogram can also beobtained by the product of two adjacent sides.
View Solution
